A stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
Consider the diagram the stone is dropped from point p.
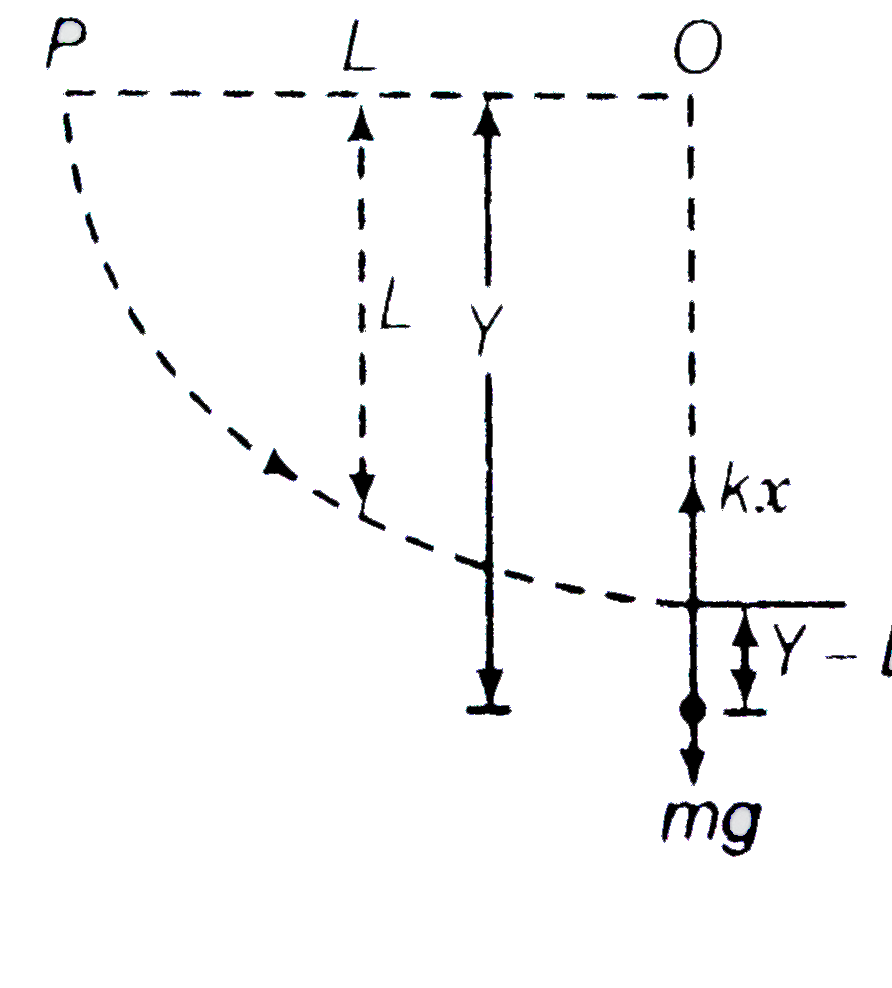
Till the stone drops through a length L it will be in free fall.
After that the elasticity of the string will force it to a SHM.
Let the stone come to rest instantaneously at y.
The loss in PE of the stone is the PE stored in the stretched string.
mgy=12k(y−L)2
⇒ mgy=12ky2−kyL+12kL2⇒12ky2−(kL+mg)y+14kL2=0
y=(kL+mg)±√(kL+mg)2−k2L2k=(kL+mg)±√2mgkL+m2g2k
Retain the positive sign.
∴ y=(kL+mg)+√2mgkL+m2g2k
(b) In SHM, the maximum velocity is attained when the body passes, through the ''equilibrium, position'' i.e., when the instantaneous acceleration is zero. That is mg−kx=0, where x is the extension from L.
⇒ mg=kx
Let the velocity be v. Then,
12mv2+12kx2=mg(L+x) (from conservation of energy)
12mv2=mg(L+x)−12kx2
Now, mg=kx⇒x=mgk
∴ 12mv2=mg(L+mgk)−12km2g2k2=mgL+m2g2k−12m2g2k
12mv2=mgL+12m2g2k
∴ v2=2gL+mg2/k
v=(2gL+mg2/k)1/2
When stone is at the lowest position i.e., at instantaneous distance y from p, then equation of motion of the stone is
md2ydt2=mg−k(y−L)⇒d2ydt2+km(y−L)−g=0
Make a transformation of variables, z=km(y−L)−g
∴ d2zdt2+kmz=0
It is differential equation of second order which represents SHM.
Comparing with equation d2zdt2+ω2z=0
Angular frequency of harmonic motion ω=√km
The solution of above equation will be of the type z=Acos(ωt+ϕ), where ω=√km
y=(L+mgk)+Acos(ωt+ϕ)
Thus, the stone will perform SHM with angular frequency ω=√k/m about a point y0=L+mgk.
Similar Questions
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View Solution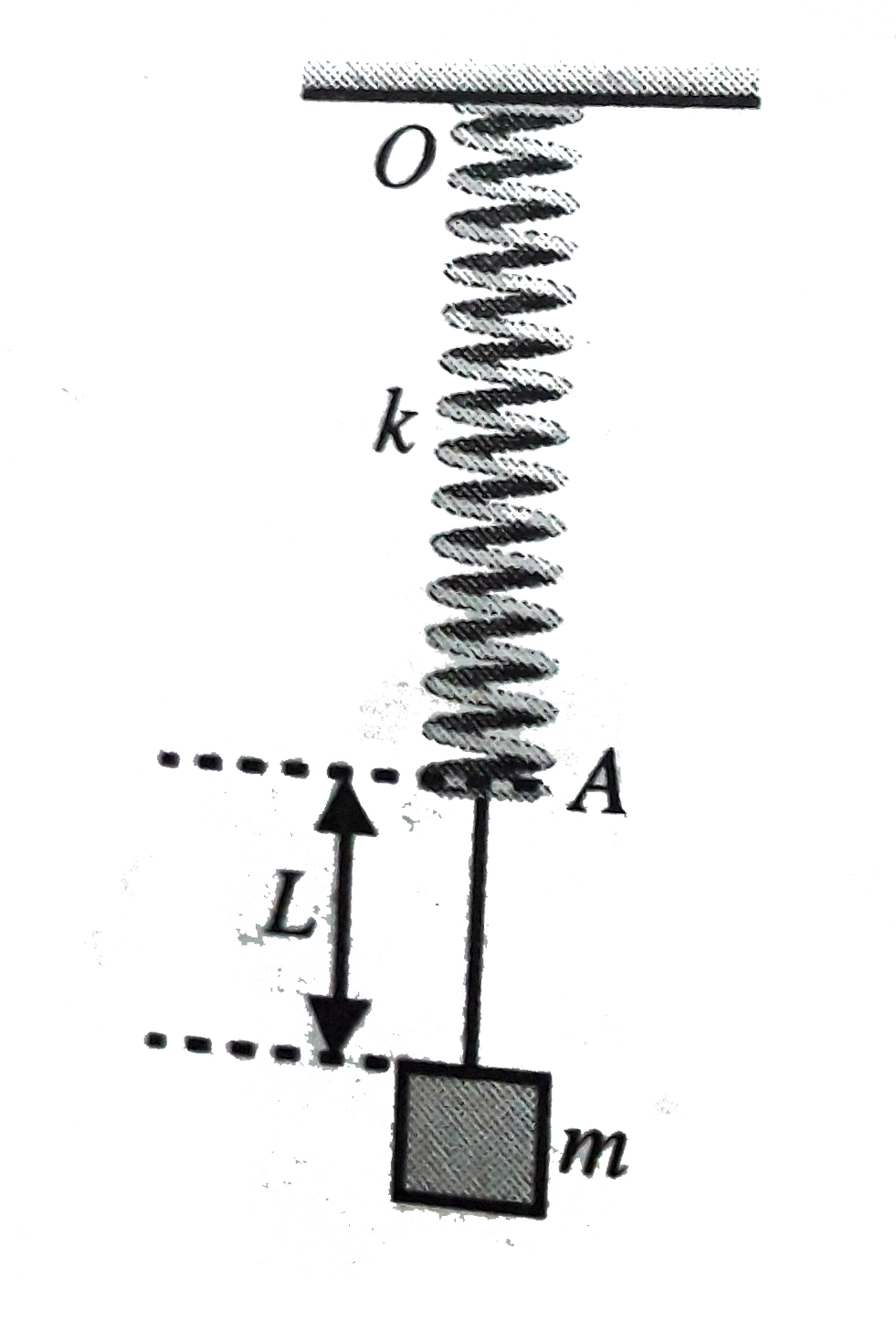
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA stone of mass 0.2 kg is tied to one end of a string of length 80 cm. Holding the other and, the stone is whiled into a vertical circle. The minimum speed of the stone and tension at the lowest point of circular path so that it just comletes the circle are
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View Solution
