The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
16√5 cm
10√5 cm
24√5 cm
28 cm
The correct Answer is:C
(c) Let ABC be a triangle in which sides AB=35 cm, BC=54 cm and CA=61 cm
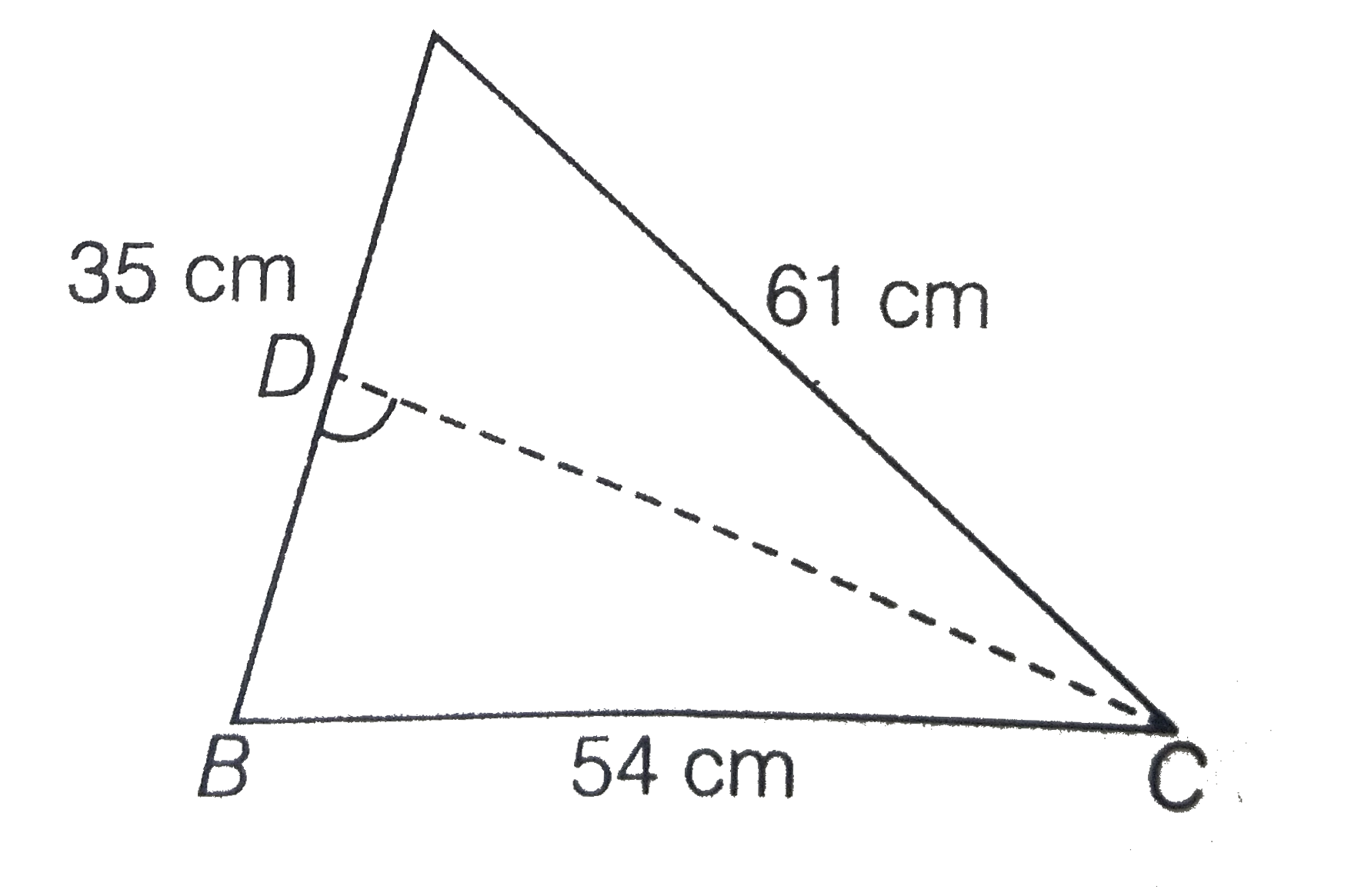
Now, semi-perimeter of a triangle,
s=a+b+c2=35+54+612=1502=75cm
[∵semi-perimeter,s=a+b+c2]
∵Area of△ABC=√s(s−a)(s−b)(s−c)
=√75(75−35)(75−54)(75−61)
=√75×40×21×14
=√25×3×4×2×5×7×3×7×2
=5×2×2×3×7√5=240√5cm2
Also, Area of△ABC=12×AB×Altitude
⇒12×35×CD=420√5
⇒CD=420×2√535
∴CD=24√5
Hence, the length of altitude is 24√5cm.
Topper's Solved these Questions
Similar Questions
The sides of a triangle are 5 cm, 8 cm and 11 cm respectively. Demtermine whether it is a right angled triangle or not.
View SolutionFind the area of a triangle whose sides are 3cm, 4cm and 5cm respectively.
View SolutionA triangle has sides 35cm,54cm and 61cm long. Find its area. Also, find the smallest of its altitudes.
View SolutionA triangle has sides 35cm,54cm and 61cm long. Find its area. Also, find the smallest of its altitudes.
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, what is the length of the longest side of the smaller triangle?
View SolutionTwo sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionIf two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
View SolutionFind the area of triangle whose sides are 5 cm, 12 cm and 13 cm. Also, find the length of its altitude corresponding to the longest side.
View SolutionFind the area of triangle whose sides are 17 cm, 8 cm and 15 cm. Also calculate the length of the altitude corresponding to the largest side of the triangle.
View Solution