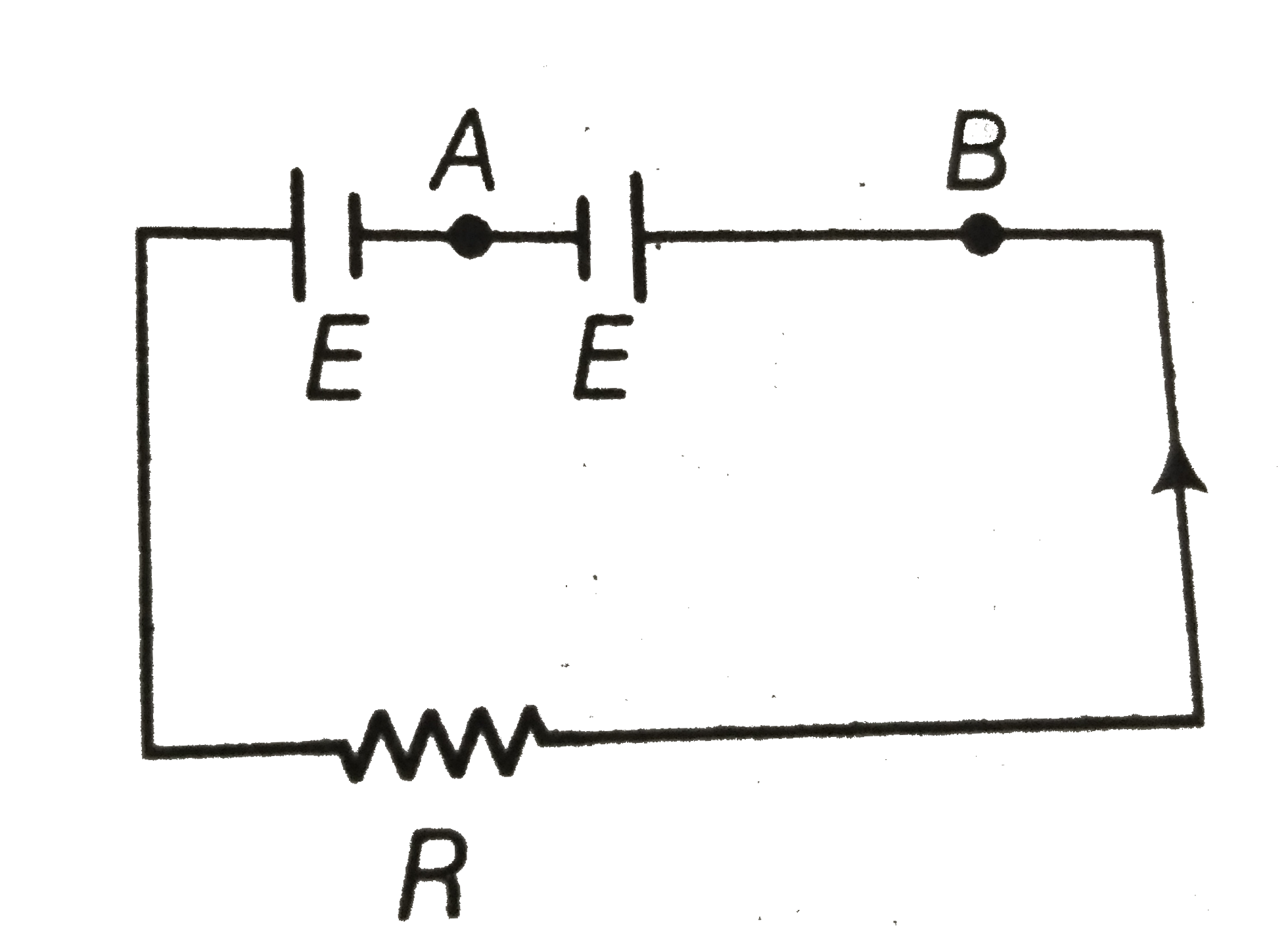
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
Applying Ohm's law
Effective resistance =R+r1+r2 and effective emf of two cells =E+E=2E, so the electric current is given by
I=E+EE+r1+r2
The potential difference across the terminals of the first cell and putting it equal to zero.
V1=E−Ir1=E−2Er1+r2+Rr1=0
or E=2Er1r1+r2+R⇒1=2r1r1+r2+R
r1+r2+R=2r1⇒R=r1−r2
this is the required relation.
Similar Questions
Two cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A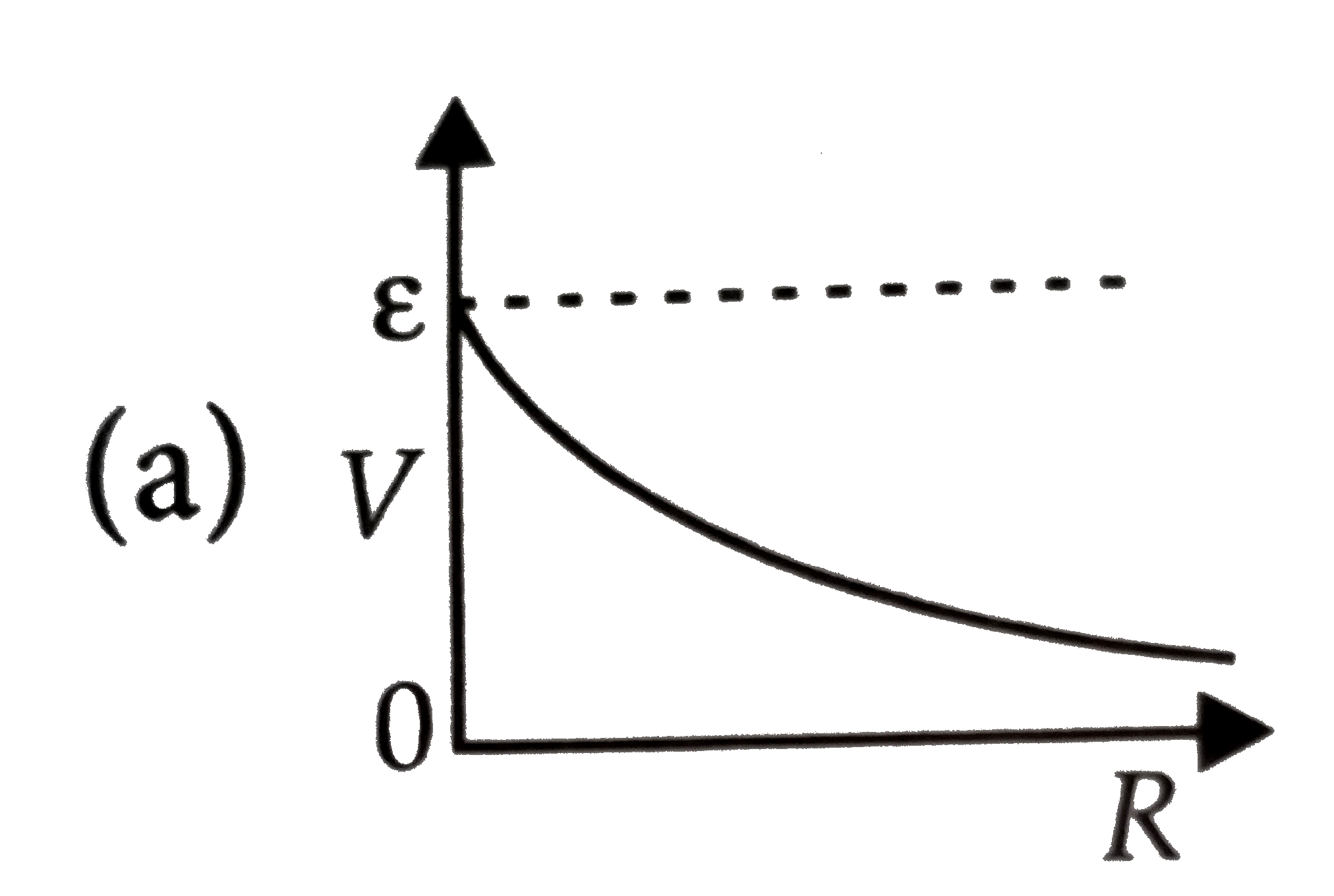 B
B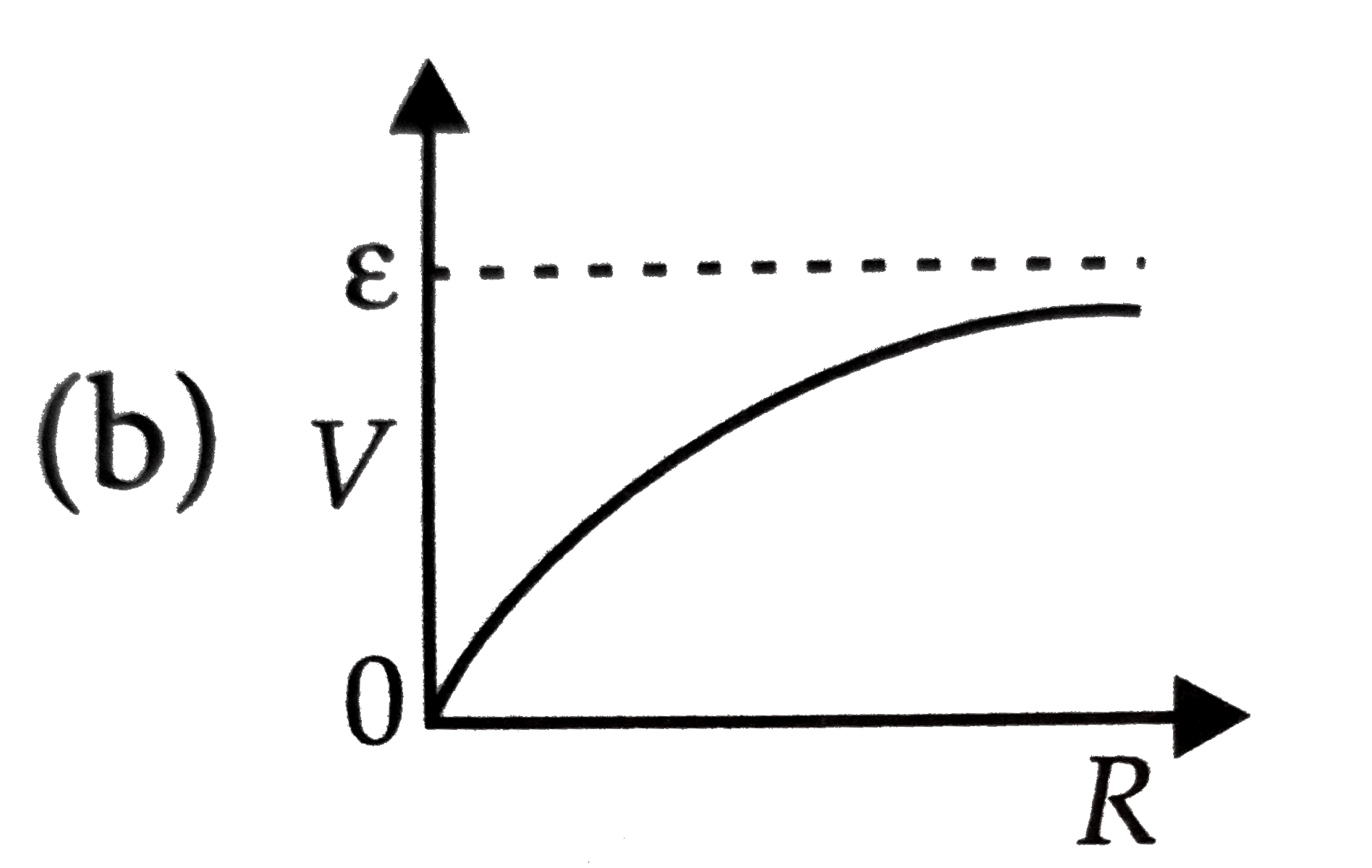 C
C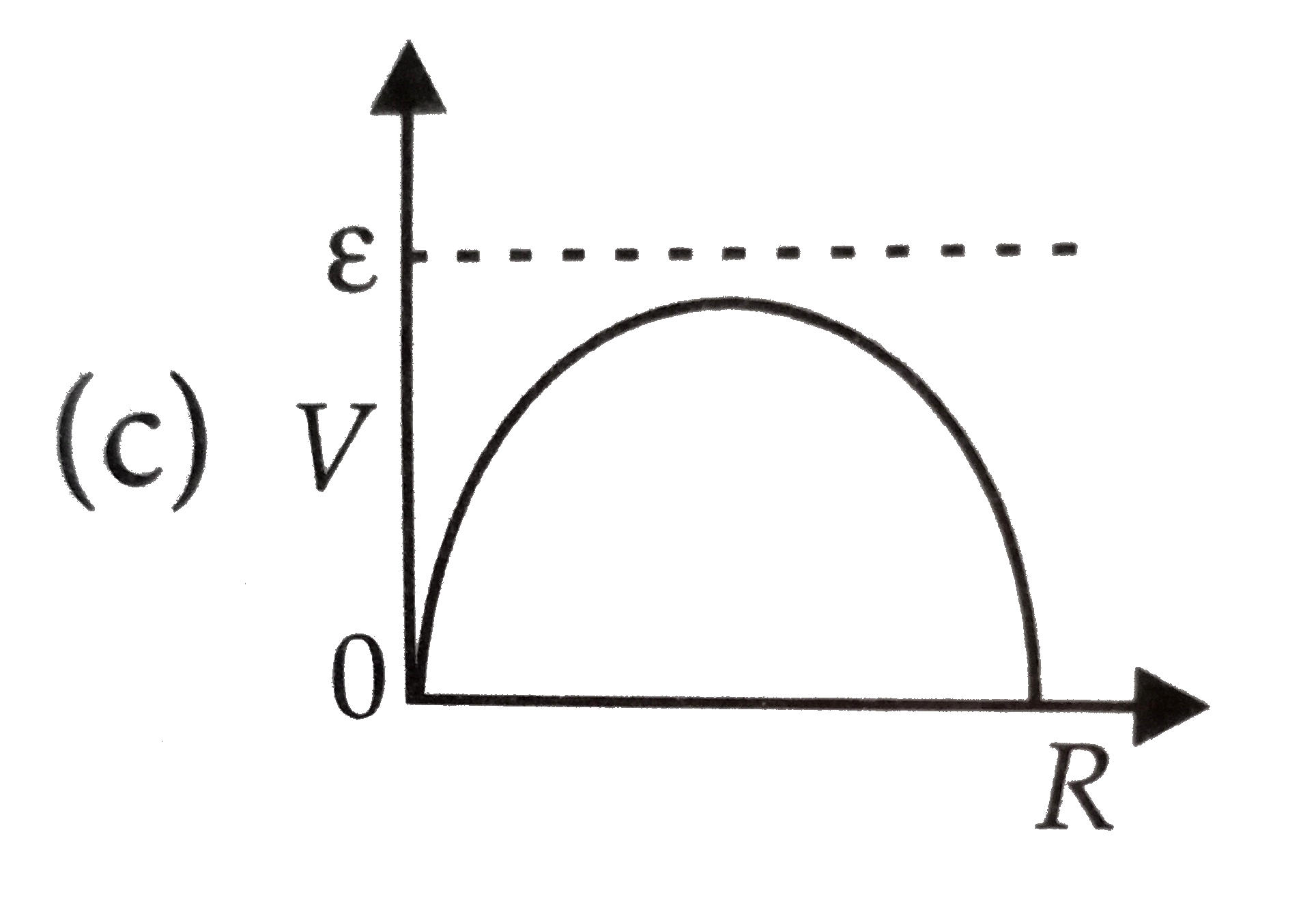 D
D
A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
View SolutionTwo sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View Solution

