If f(x)={xnsin(1x2)x≠00x=0, (n∈I), then (a) limx→0f(x) exists for n>1 (b) limx→0f(x) exists for n<0 (c) limx→0f(x) does not exist for any value of n (d) limx→0f(x) cannot be determined
To solve the problem, we need to analyze the limit of the function f(x) as x approaches 0. The function is defined as follows:
f(x)={xnsin(1x2)if x≠00if x=0
We need to evaluate the limit limx→0f(x) for different values of n.
Step 1: Evaluate the Right-Hand Limit
We start by evaluating the right-hand limit:
limx→0+f(x)=limx→0+xnsin(1x2)
As x→0+, xn approaches 0 if n>0. The sine function, sin(1x2), oscillates between -1 and 1, so it is bounded. Therefore, we can conclude:
limx→0+f(x)=0⋅(bounded)=0
Step 2: Evaluate the Left-Hand Limit
Next, we evaluate the left-hand limit:
limx→0−f(x)=limx→0−xnsin(1x2)
Similar to the right-hand limit, as x→0−, xn approaches 0 if n>0. The sine function remains bounded. Thus, we have:
limx→0−f(x)=0⋅(bounded)=0
Step 3: Conclusion for n≥1
Since both the right-hand limit and the left-hand limit equal 0, we conclude that:
limx→0f(x)=0for n≥1
Step 4: Consider n<0
If n<0, as x→0, xn approaches infinity. The sine function still oscillates between -1 and 1. Therefore, the limit does not exist because f(x) does not approach a finite value.
Final Conclusion
- For n>1: The limit exists and equals 0.
- For n<0: The limit does not exist.
- For n=1: The limit exists and equals 0.
Answer Selection
Based on the analysis:
- (a) True: limx→0f(x) exists for n≥1.
- (b) False: limx→0f(x) does not exist for n<0.
- (c) False: limx→0f(x) exists for n≥1.
- (d) False: The limit can be determined.
Thus, the correct option is (a).
- For n<0: The limit does not exist.
- For n=1: The limit exists and equals 0.
- (b) False: limx→0f(x) does not exist for n<0.
- (c) False: limx→0f(x) exists for n≥1.
- (d) False: The limit can be determined.
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
- LINEAR INEQUALITIESBook:CENGAGE ENGLISHChapter:LINEAR INEQUALITIESExercise:All Questions
Explore 68 Videos
Similar Questions
limx→0xsecx
View Solutionlimx→0(x3logx)
View Solutionlimx→0sinxx=?
View Solutionlimx→0(x2−3x+2)
View SolutionIf f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
View SolutionEvaluate limx→0f(x), where
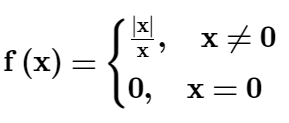
View SolutionEvaluate: limx→0xx
View Solutionlimx→0x2−xsinx
View Solutionlimx→0(1−cosxx2)
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View Solution
