Let S be the area bounded by the curve y=sinx(0≤x≤π) and the x-axis and T be the area bounded by the curves y=sinx(0≤x≤π2),y=acosx(0≤x≤π2), and the x-axis (wherea∈R+) The value of (3a) such that S:T=1:13 is______
The correct Answer is:4
We have S=πsinx0dx=2,soT=23, where a>0.
Now T=tan−1a∫0sinxdx+π/2∫tan−1aacosxdx=23
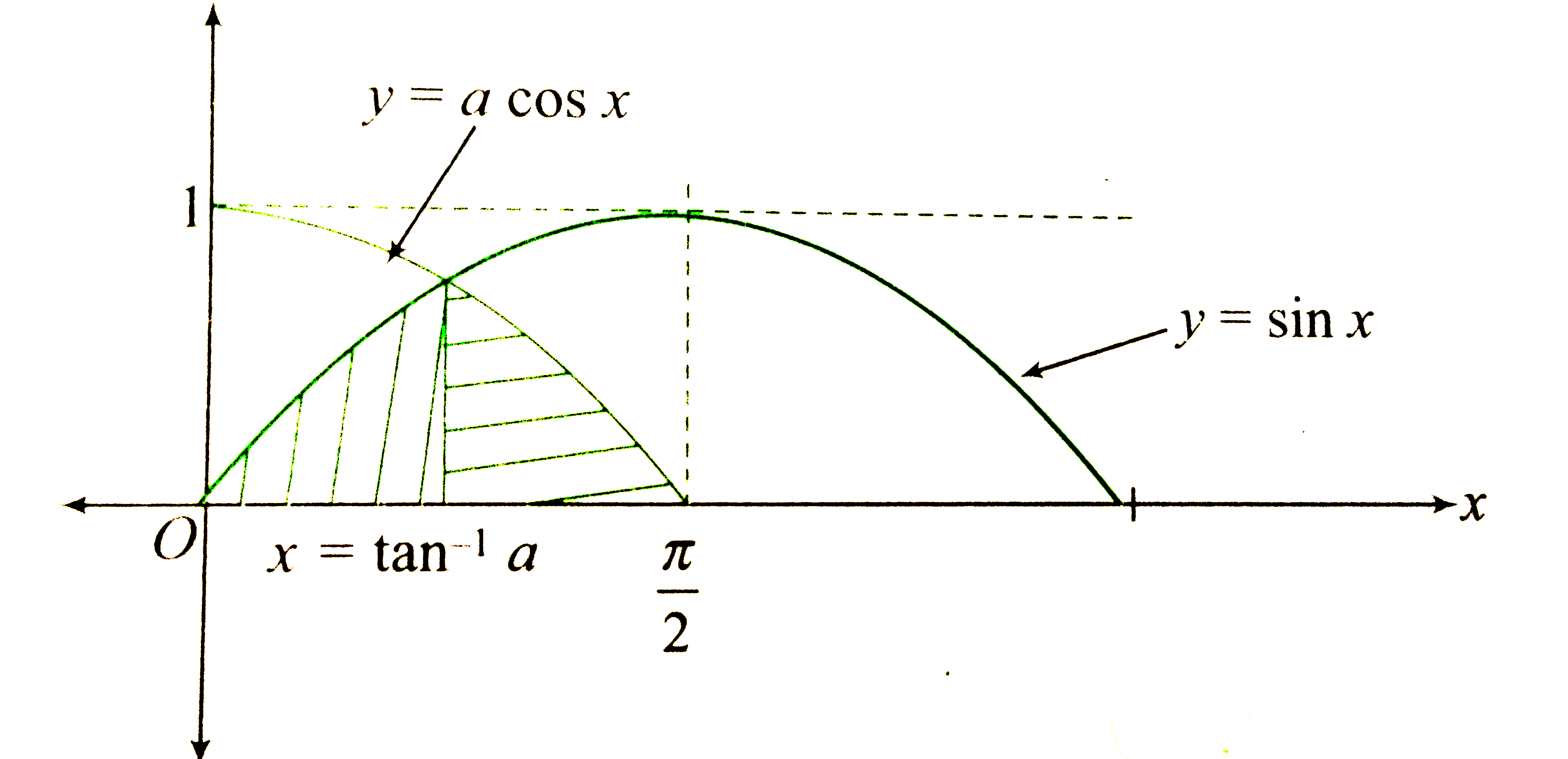
i.e.,−cos(tan−1a)+1+a{[1−sin(tan−1a)]}=23
i.e.,−1√1+x2+1+a−a2√1+a2=23
or (a+1)−√a2+1=23ora+13=√a2+1
or a=43
Hence, 3a=4.
Topper's Solved these Questions
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Archives
Explore 10 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Single Correct Answer Type
Explore 30 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Matrix Match Type
Explore 5 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
Similar Questions
The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the X-axis is
View SolutionLet the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
View SolutionMatch the following lists :

View SolutionA lamp post of length 10 meter placed at the end A of a ladder AB of length 13 meters, which is leaning against a vertical wall as shown in figure and its base slides away from the wall. At the instant base B is 12 m from the vertical wall, the base B is moving at the rate of 5 m/sec. A man (M) of height 1.5 meter standing at a distance of 15 m from the vertical wall.

Rate at which θ decreases, when the base B is 12 m from the vertical wall, is
View SolutionConsider set A={T(r+1)=.nCr(3)n−r(5x)r,r=0,1,23,…..,n}. Match the following lists :

View SolutionThe area bounded by the y-axis, y=cosxand y=s∈xwhen 0≤x≤π2is(A) 2(√2−1) (B) √2−1 (C) √2+1 (D) √2
View SolutionFind the area of the region bounded by the x-axis and the curves defined by y=tanx(where−π3≤x≤π3) and y=cotx(whereπ6≤x≤3x2) .
View SolutionEvaluate the following integral: ∫90f(x)dx, where f(x){sinx, 0≤x≤π/21,π2≤x≤3ex−3, 3≤x≤9
View SolutionSolve the equation (sinx+cosx)1+sin2x=2, when 0≤x≤π
View SolutionIf f(x)=∫π0tsintdt√1+tan2xsin2t for 0<x<π2 then
View SolutionFind the area of the region bounded by the curve y=sinx, the lines x=−π2,x=π2 and X- axis.
View SolutionLet the curve y=ax12 +bx passes through the point (1,2) and lies above the axis for 0<x<9 .If the area enclosed by the curve the x-axis and the line x =4 is 8 eq. units Then-
View SolutionLet S be the area bounded by the curve y=sinx(0≤x≤π) and the x-axis and T be the area bounded by the curves y=sinx(0≤x≤π2),y=acosx(0≤x≤π2), and the x-axis (wherea∈R+) The value of (3a) such that S:T=1:13 is______
View SolutionFind the area bounded by the y-axis, y=cosx ,and y=sinx when 0≤x≤π2.
View SolutionFind the area of the region bounded by the x-axis and the curves defined by y=tanx(where−π3≤x≤π3) and y=cotx(whereπ6≤x≤3x2) .
View SolutionIf f(x)=∫π0tsintdt√1+tan2xsin2t for 0<x<π2 then
View Solution
