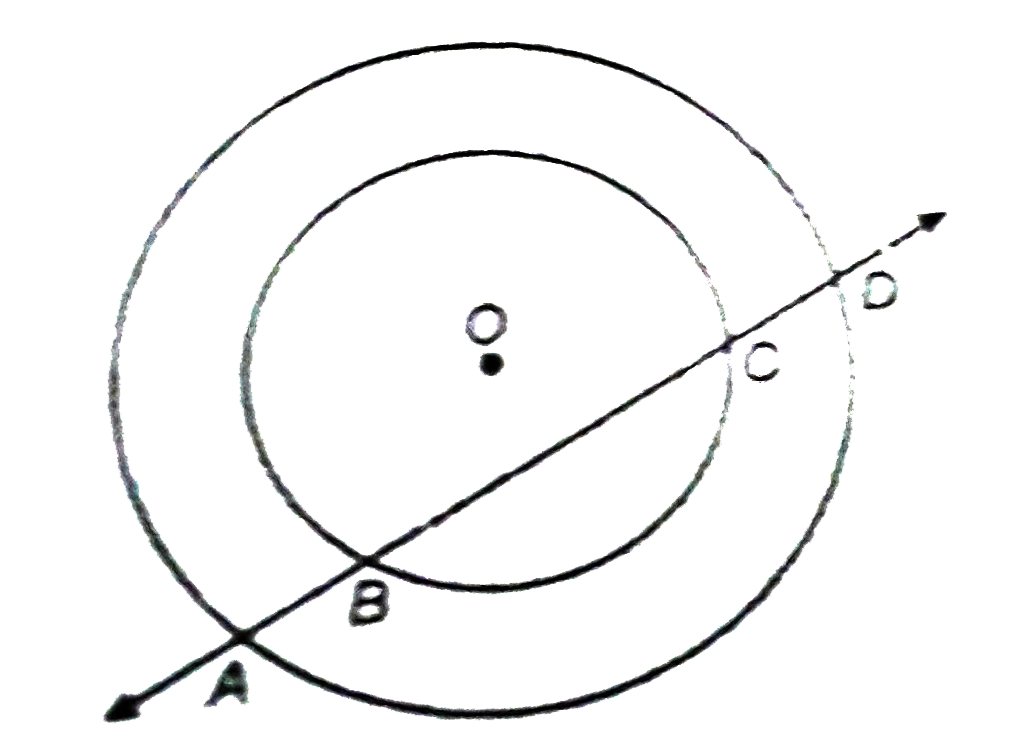
In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A,B,C and D . Show that AB=CD.
To solve the problem, we need to show that the length of chord AB in the larger circle is equal to the length of chord CD in the smaller circle. Here’s a step-by-step solution:
Step 1: Identify the Setup
We have two concentric circles with a common center O. The line l intersects the larger circle at points A and B, and the smaller circle at points C and D.
Hint: Remember that concentric circles share the same center.
Step 2: Draw Perpendiculars
Draw a perpendicular line from the center O to the chords AB and CD. Let the perpendicular from O to chord AB meet AB at point M, and the perpendicular from O to chord CD meet CD at point N.
Hint: The property of circles states that a perpendicular from the center to a chord bisects the chord.
Step 3: Apply the Bisecting Property
Since OM is perpendicular to AB, we have:
- AM = MB (let’s call this length x)
Similarly, since ON is perpendicular to CD, we have:
- CN = ND (let’s call this length y)
Hint: Use the property of perpendiculars from the center to chords to establish equal segments.
Step 4: Relate the Chords
From the properties established:
- The length of chord AB can be expressed as:
AB=AM+MB=x+x=2x
- The length of chord CD can be expressed as:
CD=CN+ND=y+y=2y
Hint: Recognize that both chords can be expressed in terms of their respective segments.
Step 5: Show Equality
Since both chords are bisected by the perpendiculars from the center, we can conclude that:
- The distance from the center O to the chords is the same (since they are concentric), thus:
AM=CNandMB=ND
This implies that:
AB=CD
Hint: The equality of the segments derived from the center leads to the conclusion about the lengths of the chords.
Conclusion
Thus, we have shown that:
AB=CD
This completes the proof that the lengths of the chords AB and CD are equal.
---
We have two concentric circles with a common center O. The line l intersects the larger circle at points A and B, and the smaller circle at points C and D.
Draw a perpendicular line from the center O to the chords AB and CD. Let the perpendicular from O to chord AB meet AB at point M, and the perpendicular from O to chord CD meet CD at point N.
Since OM is perpendicular to AB, we have:
- AM = MB (let’s call this length x)
- CN = ND (let’s call this length y)
From the properties established:
- The length of chord AB can be expressed as:
AB=AM+MB=x+x=2x
- The length of chord CD can be expressed as:
CD=CN+ND=y+y=2y
Since both chords are bisected by the perpendiculars from the center, we can conclude that:
- The distance from the center O to the chords is the same (since they are concentric), thus:
AM=CNandMB=ND
This implies that:
AB=CD
Thus, we have shown that:
AB=CD
Topper's Solved these Questions
Similar Questions
In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A, B, C and D . Show that AB=CD.
View SolutionIf a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC.
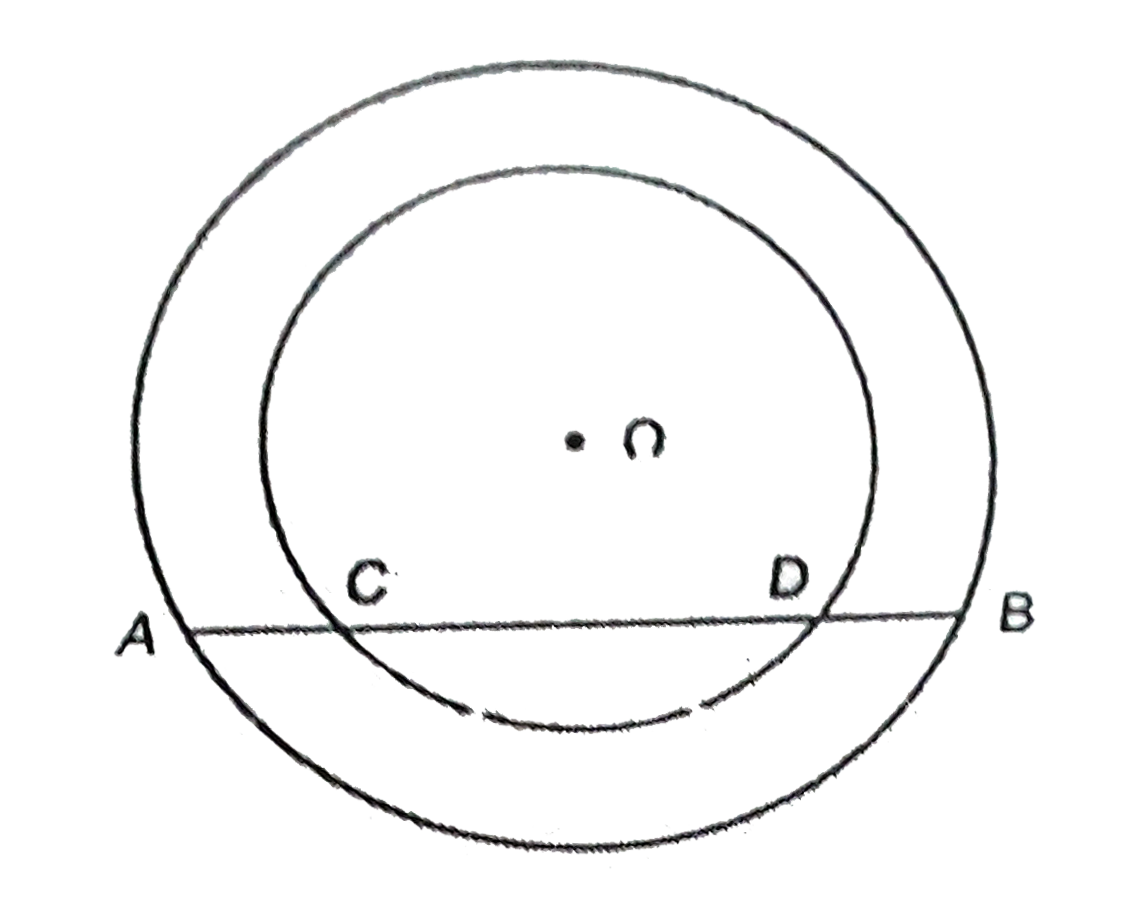
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View Solution