In the given figure,three circles of radius 2 cm touch one another externally.These circles are circumscribed by a circle of radius R cm.Find the approximate value of R.
To find the radius R of the larger circle that circumscribes three smaller circles of radius 2 cm that touch each other externally, we can follow these steps:
1. Understanding the Configuration:
We have three circles, each with a radius of 2 cm, touching each other externally. The centers of these circles form an equilateral triangle.
2. Finding the Side Length of the Triangle:
Since the radius of each circle is 2 cm, the distance between the centers of any two circles (which is the side length of the triangle) is:
AB=2+2=4 cm
Thus, each side of the equilateral triangle ABC is 4 cm.
3. Calculating the Height of the Triangle:
To find the height AD of the equilateral triangle, we can drop a perpendicular from point A to the midpoint D of side BC. The length of BD (half of BC) is:
BD=42=2 cm
Using the Pythagorean theorem in triangle ABD:
AB2=AD2+BD2
Substituting the known values:
42=AD2+2216=AD2+4AD2=16−4=12AD=√12=2√3 cm
4. Finding the Center of the Circumscribing Circle:
Let O be the center of the circumscribing circle. The distance from O to the midpoint D is 23 of the height AD:
OA=23×AD=23×2√3=4√33 cm
5. Calculating the Radius R:
The radius R of the larger circle is the distance OA plus the radius of the smaller circles:
R=OA+2=4√33+2
To combine these, we convert 2 into a fraction:
R=4√33+63=4√3+63
6. Approximating the Value of R:
To find the approximate value of R, we can use √3≈1.732:
R≈4×1.732+63=6.928+63=12.9283≈4.309 cm
Final Answer:
The approximate value of R is 4.309 cm.
We have three circles, each with a radius of 2 cm, touching each other externally. The centers of these circles form an equilateral triangle.
Since the radius of each circle is 2 cm, the distance between the centers of any two circles (which is the side length of the triangle) is:
AB=2+2=4 cm
Thus, each side of the equilateral triangle ABC is 4 cm.
To find the height AD of the equilateral triangle, we can drop a perpendicular from point A to the midpoint D of side BC. The length of BD (half of BC) is:
BD=42=2 cm
Using the Pythagorean theorem in triangle ABD:
AB2=AD2+BD2
Substituting the known values:
42=AD2+2216=AD2+4AD2=16−4=12AD=√12=2√3 cm
Let O be the center of the circumscribing circle. The distance from O to the midpoint D is 23 of the height AD:
OA=23×AD=23×2√3=4√33 cm
The radius R of the larger circle is the distance OA plus the radius of the smaller circles:
R=OA+2=4√33+2
To combine these, we convert 2 into a fraction:
R=4√33+63=4√3+63
To find the approximate value of R, we can use √3≈1.732:
R≈4×1.732+63=6.928+63=12.9283≈4.309 cm
The approximate value of R is 4.309 cm.
Topper's Solved these Questions
Similar Questions
Find the middle term of the A.P. 213, 205, 197, ..., 37.
View SolutionIn the given figure,three circles of radius 2cm touch one another externally.These circles are circumscribed by a circle of radius Rcm. Find the approximate value of R .
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionConsider the circle S=x^(2)+y^(2)-4x-4y+4=0. If another circle of radius r'r' less than the radius of the circle S is drawn,touching the circles,and the coordinate axes,then the value of r' is
View SolutionAs shown in the figure,the five circles are tangent to one another consecutively and to the lines L_(1) and L_(2). If the radius of the largest circle is 18 and that of smallest is 8. If radius of middle circle is r, then find the value of r/2
View SolutionCircles of radii 2,2,1 touch each other externally.If a circle of radius r touches all the three circles externally,then r is
View SolutionThree equal circles each of radius 1 cm are circumscribed by a larger circle. Find the perimeter of the circumscribing circle :
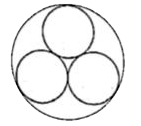
View SolutionSix circles each of unit radius are being circumscribed by another larger circle. All the smaller circles touch each other . What is the circumference of the larger circle ?
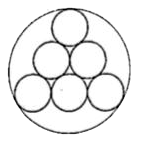
View SolutionIn a quadrant ( of a circle ) a circle of maximum possible area is given . If the radius of the circumscribing quadrant be r, then what is the area of the inscribed circle ?
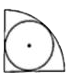
View SolutionThree equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionThe radius R Find the point of the center of a circle, if this circle, R The outer circle touches the second circle of radius.
View SolutionAs show in the figure , the five circles are tangent to one another consecutively and to the lines L1andL2. If the radius of the largest circle is 18 and that of the smaller one is 8, if radius of the middle circle is r, then find the value of r/2.

View SolutionThree equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
View SolutionIn the following diagram there are three circles packed in another circle, such that each circle is tangent to all other circles in this arrangement. The radius of the circumscribing circle A is 1 cm, and circle B and circle C are congruent. Find the radius of the circle D.

View Solution