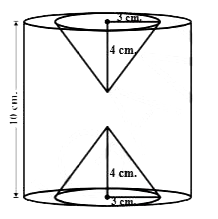
Height of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
To solve the problem, we will follow these steps:
Step 1: Find the Volume of the Cylinder
The formula for the volume V of a cylinder is given by:
V=πr2h
where r is the radius and h is the height.
Given:
- Height h=10 cm
- Diameter d=8 cm, so the radius r=d2=82=4 cm
Now, substituting the values into the formula:
V=π(4)2(10)=π(16)(10)=160πcm3
Using π≈227:
V≈160×227=35207≈502.86cm3
Step 2: Find the Volume of One Conical Hole
The formula for the volume V of a cone is given by:
V=13πr2h
where r is the radius of the base and h is the height.
Given:
- Height of the cone hc=4 cm
- Diameter of the hole dc=6 cm, so the radius rc=dc2=62=3 cm
Now, substituting the values into the formula:
Vc=13π(3)2(4)=13π(9)(4)=363π=12πcm3
Using π≈227:
Vc≈12×227=2647≈37.71cm3
Step 3: Find the Volume of the Remaining Solid
The volume of the remaining solid VR is given by:
VR=V−2Vc
Substituting the values we found:
VR=502.86−2×37.71
Calculating 2×37.71:
2×37.71≈75.42
Now substituting back:
VR=502.86−75.42≈427.44cm3
Final Answers:
1. Volume of the cylinder: 502.86cm3
2. Volume of one conical hole: 37.71cm3
3. Volume of the remaining solid: 427.44cm3
---
The formula for the volume V of a cylinder is given by:
V=πr2h
where r is the radius and h is the height.
- Height h=10 cm
- Diameter d=8 cm, so the radius r=d2=82=4 cm
V=π(4)2(10)=π(16)(10)=160πcm3
Using π≈227:
V≈160×227=35207≈502.86cm3
The formula for the volume V of a cone is given by:
V=13πr2h
where r is the radius of the base and h is the height.
- Height of the cone hc=4 cm
- Diameter of the hole dc=6 cm, so the radius rc=dc2=62=3 cm
Vc=13π(3)2(4)=13π(9)(4)=363π=12πcm3
Using π≈227:
Vc≈12×227=2647≈37.71cm3
The volume of the remaining solid VR is given by:
VR=V−2Vc
Substituting the values we found:
VR=502.86−2×37.71
Calculating 2×37.71:
2×37.71≈75.42
Now substituting back:
VR=502.86−75.42≈427.44cm3
1. Volume of the cylinder: 502.86cm3
2. Volume of one conical hole: 37.71cm3
3. Volume of the remaining solid: 427.44cm3
Topper's Solved these Questions
Similar Questions
Find the median of the following data: class : 0−10,equency:5, 10−20,3, 20−30,4, 30−40,3, 40−50,3,50-60 , 4,60-70 , 7, 70-80 , 9,80-90 , 7,90-100 , 8,
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionThe height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
View SolutionHeight of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
View SolutionThe height of a solid cylinder is 15 cm. and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm, and height 4 cm are cut off. Find the volume of the remaining solid.
View SolutionThe height of a solid cylindr is 15 cm and diameter is 7 cm .Two equal conical holes of radius 3 cm and height 4 cm are cut off . Find the volume and surface area of the solid.
View Solutionऊचाई 12 cm और व्यास 10 cm वाले एक ठोस बेलन में से इसी ऊँचाई एवं व्यास बाला एक शंक्वाकार खोल (cavity) काट लिया जाता है । शेष बचे भाग का आयतन ज्ञात करें।
View Solutionएक ठोस लंबवृत्तीय बेलन के दोनों सिरों में शंक्वाकार छेद किये जाते है। बेलन की लम्बाई 10 सेमी तथा आधार का व्यास 8 सेमी है। यदि दोनों सिरों के छेद का व्यास 6 सेमी तथा गहराई 4 सेमी हो तो शेष आकृति का सम्पूर्ण पृष्ठ और आयतन ज्ञात कीजिए।
View Solutionएक ठोस बेलन की ऊंचाई 15 सेमी और व्यास 7 सेमी है इसमें से 3 सेमी त्रिज्या और 4 सेमी ऊंचाई के दो शक्वाकार भाग निकाल दिए जाते है । शेष ठोस का आयतन और सम्पूर्ण पृष्ठ ज्ञात कीजिए ।
View SolutionIn the adjacent figure, the height of a solid cylinder is 10 cm and diameter is 7 cm. Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown in the figure. Find the volume of the remaining solid.
View SolutionIn the adjacent figure, the height of a solid cylinder is 10 cm and diameter is 7 cm. Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown in the figure. Find the volume of the remaining solid.
View SolutionIn the adjacent figure, the height of a solid cylinder is 10 cm and diameters is 7 cm . Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown the figure. Find the volume of the remaining solid.
View SolutionThe height of a solid cylinder is 15 cm and the diameter of the base is 7 cm. It has two conical pits of 3 cm radius and 4 cm height. Find the volume of the remaining solid.
View SolutionIn the adjacent figure, the height of a solid cylinder is 10 cm and diameters is 7 cm . Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown the figure. Find the volume of the remaining solid.
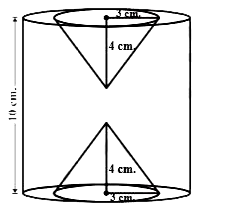
View SolutionThe height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
View Solution