A villager Itwari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of plot from one of the corners to construct a Health centre. Itwari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how his proposal will be implemented.
To implement Itwari's proposal of exchanging a portion of his quadrilateral plot for an adjoining triangular plot, we can follow these steps:
1. Identify the Quadrilateral Plot:
Let the quadrilateral plot owned by Itwari be represented as ABCD.
2. Draw Diagonals:
Draw the diagonal AC to help visualize the triangles that will be formed.
3. Construct a Parallel Line:
From point D, draw a line DE parallel to AC. This will help in creating the necessary triangles.
4. Identify the Area for Health Centre:
The Gram Panchayat will take over the area EDC for constructing the health center.
5. Determine the Remaining Area:
The area left after the Gram Panchayat takes over is the area ECB.
6. Prove Area Equality:
To prove that the area of the old land (ABCD) is equal to the area of the new triangular land (ECB), we need to show that the area of triangle ACD is equal to the area of triangle ACE.
7. Use Properties of Triangles:
Since triangles ACD and ACE share the same base AC and are between the same parallel lines AC and DE, we can conclude that:
Area of △ACD=Area of △ACE
8. Add Areas:
Now, add the area of triangle ABC to both sides:
Area of ABC+Area of ACD=Area of ABC+Area of ACE
9. Combine Areas:
The left side becomes the area of quadrilateral ABCD, and the right side becomes the area of triangle EBC:
Area of ABCD=Area of EBC
10. Conclusion:
Thus, we have shown that the area of the old land (ABCD) is equal to the area of the new triangular land (EBC), satisfying Itwari's condition.
Let the quadrilateral plot owned by Itwari be represented as ABCD.
Draw the diagonal AC to help visualize the triangles that will be formed.
From point D, draw a line DE parallel to AC. This will help in creating the necessary triangles.
The Gram Panchayat will take over the area EDC for constructing the health center.
The area left after the Gram Panchayat takes over is the area ECB.
To prove that the area of the old land (ABCD) is equal to the area of the new triangular land (ECB), we need to show that the area of triangle ACD is equal to the area of triangle ACE.
Since triangles ACD and ACE share the same base AC and are between the same parallel lines AC and DE, we can conclude that:
Area of △ACD=Area of △ACE
Now, add the area of triangle ABC to both sides:
Area of ABC+Area of ACD=Area of ABC+Area of ACE
The left side becomes the area of quadrilateral ABCD, and the right side becomes the area of triangle EBC:
Area of ABCD=Area of EBC
Thus, we have shown that the area of the old land (ABCD) is equal to the area of the new triangular land (EBC), satisfying Itwari's condition.
Topper's Solved these Questions
Similar Questions
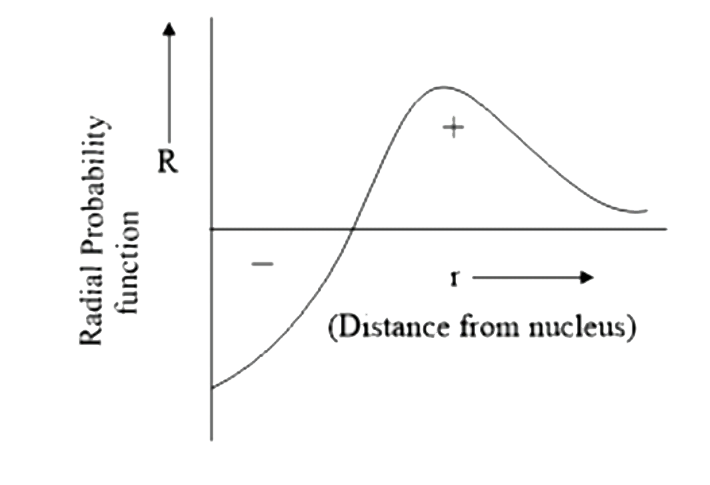
Number of nodes in above plot is
View SolutionArea of a square plot is 2304m2. Find the side of the square plot.
View SolutionAccording to Darwin one acre of land may contain
View SolutionA piece of land is in the shape of an equilateral triangle. Its boundary has to be fenced with barbed wire. What is the length of the barbed wire required?
View SolutionIn the adjoining plot of land , all the adjacent side are at right angles . Find
the area of the plot .
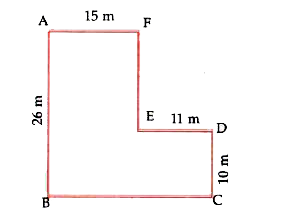
View SolutionA plot has the shape of a square. Its one side is 24 m long.
Calculate its perimeter.
View SolutionIn land animals blood vascular system has
View SolutionA plot has the shape of a square. Its one side is 24 m long.
What will be the cost of fencing the plot at ₹ 20 per metre?
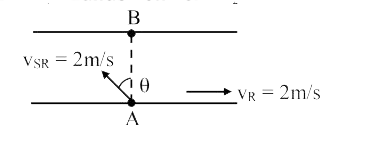
View SolutionFind θ in the given situation so that the swimmer directly lands on the point B.
View SolutionPlot y=x+sinx.
View Solution