Compute the area of trapezium PQRS in the given figure.
To compute the area of trapezium PQRS, we will break it down into two parts: the area of rectangle PSRT and the area of triangle QRT.
1. Identify the Components:
- We know that trapezium PQRS can be divided into rectangle PSRT and triangle QRT.
- Let’s denote the lengths:
- QT = 8 cm (the length of the base of triangle QRT)
- RT = height of triangle QRT (which we need to find).
2. Calculate the Area of Rectangle PSRT:
- The area of a rectangle is given by the formula:
Area=Base×Height
- Here, the base PS = QT = 8 cm and the height PSRT = RT.
- Therefore, the area of rectangle PSRT is:
Area of PSRT=QT×RT=8×RT
3. Calculate the Area of Triangle QRT:
- The area of a triangle is given by the formula:
Area=12×Base×Height
- Here, the base QT = 8 cm and the height is RT.
- Therefore, the area of triangle QRT is:
Area of QRT=12×QT×RT=12×8×RT=4RT
4. Combine the Areas:
- Now, we can find the total area of trapezium PQRS by adding the areas of rectangle PSRT and triangle QRT:
Area of PQRS=Area of PSRT+Area of QRT=8RT+4RT=12RT
5. Find RT using Pythagorean Theorem:
- In triangle QRT, we can use the Pythagorean theorem:
QR2=QT2+RT2
- Given QR = 17 cm and QT = 8 cm, we can substitute:
172=82+RT2⟹289=64+RT2
- Rearranging gives:
RT2=289−64=225
- Taking the square root:
RT=√225=15 cm
6. Calculate the Final Area:
- Substitute RT back into the area formula:
Area of PQRS=12RT=12×15=180 cm2
Final Answer:
The area of trapezium PQRS is 180 cm2.
- We know that trapezium PQRS can be divided into rectangle PSRT and triangle QRT.
- Let’s denote the lengths:
- QT = 8 cm (the length of the base of triangle QRT)
- RT = height of triangle QRT (which we need to find).
- The area of a rectangle is given by the formula:
Area=Base×Height
- Here, the base PS = QT = 8 cm and the height PSRT = RT.
- Therefore, the area of rectangle PSRT is:
Area of PSRT=QT×RT=8×RT
- The area of a triangle is given by the formula:
Area=12×Base×Height
- Here, the base QT = 8 cm and the height is RT.
- Therefore, the area of triangle QRT is:
Area of QRT=12×QT×RT=12×8×RT=4RT
- Now, we can find the total area of trapezium PQRS by adding the areas of rectangle PSRT and triangle QRT:
Area of PQRS=Area of PSRT+Area of QRT=8RT+4RT=12RT
- In triangle QRT, we can use the Pythagorean theorem:
QR2=QT2+RT2
- Given QR = 17 cm and QT = 8 cm, we can substitute:
172=82+RT2⟹289=64+RT2
- Rearranging gives:
RT2=289−64=225
- Taking the square root:
RT=√225=15 cm
- Substitute RT back into the area formula:
Area of PQRS=12RT=12×15=180 cm2
The area of trapezium PQRS is 180 cm2.
Topper's Solved these Questions
Similar Questions
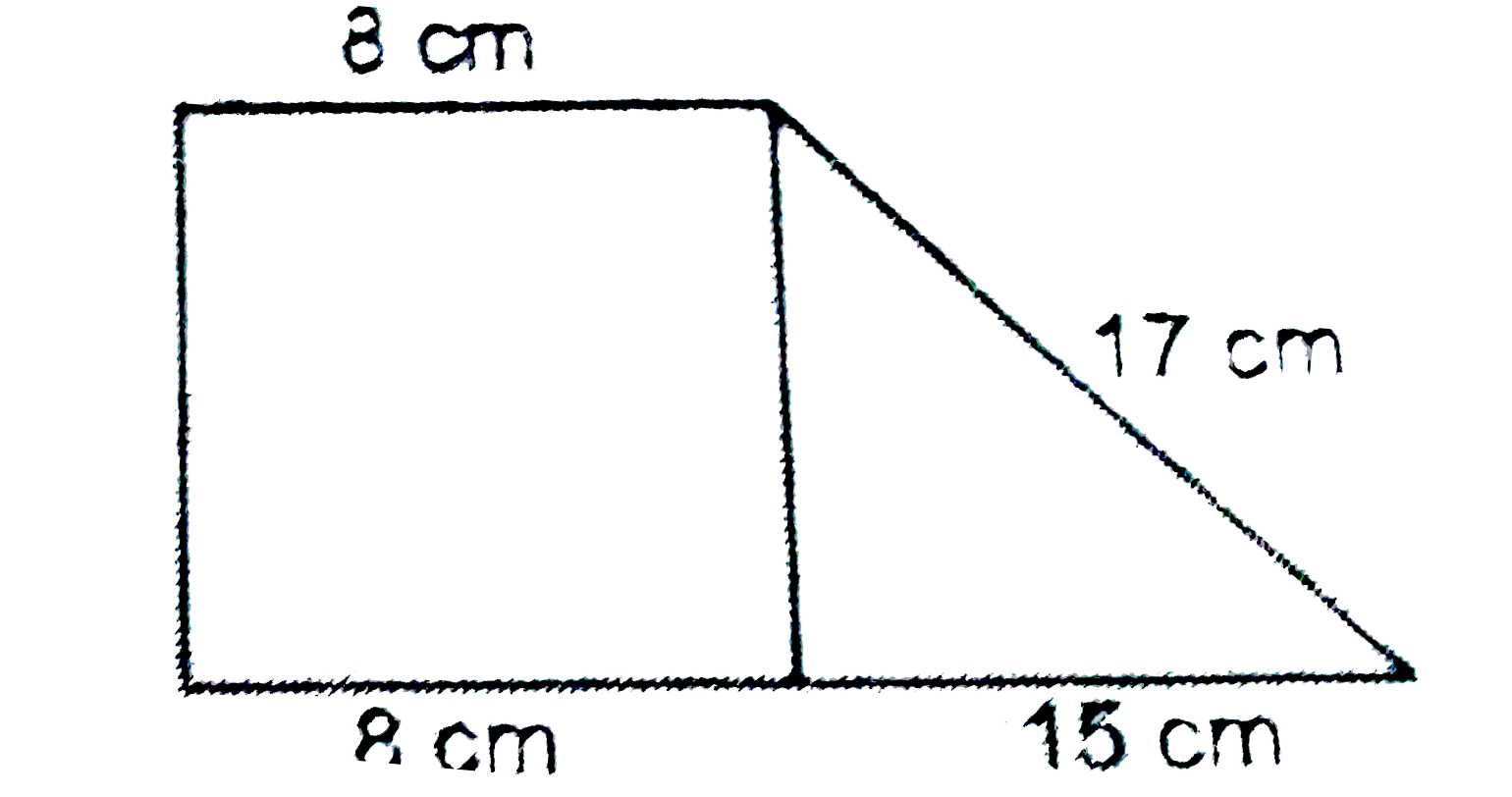
Find the area of trapezium in the given figure.
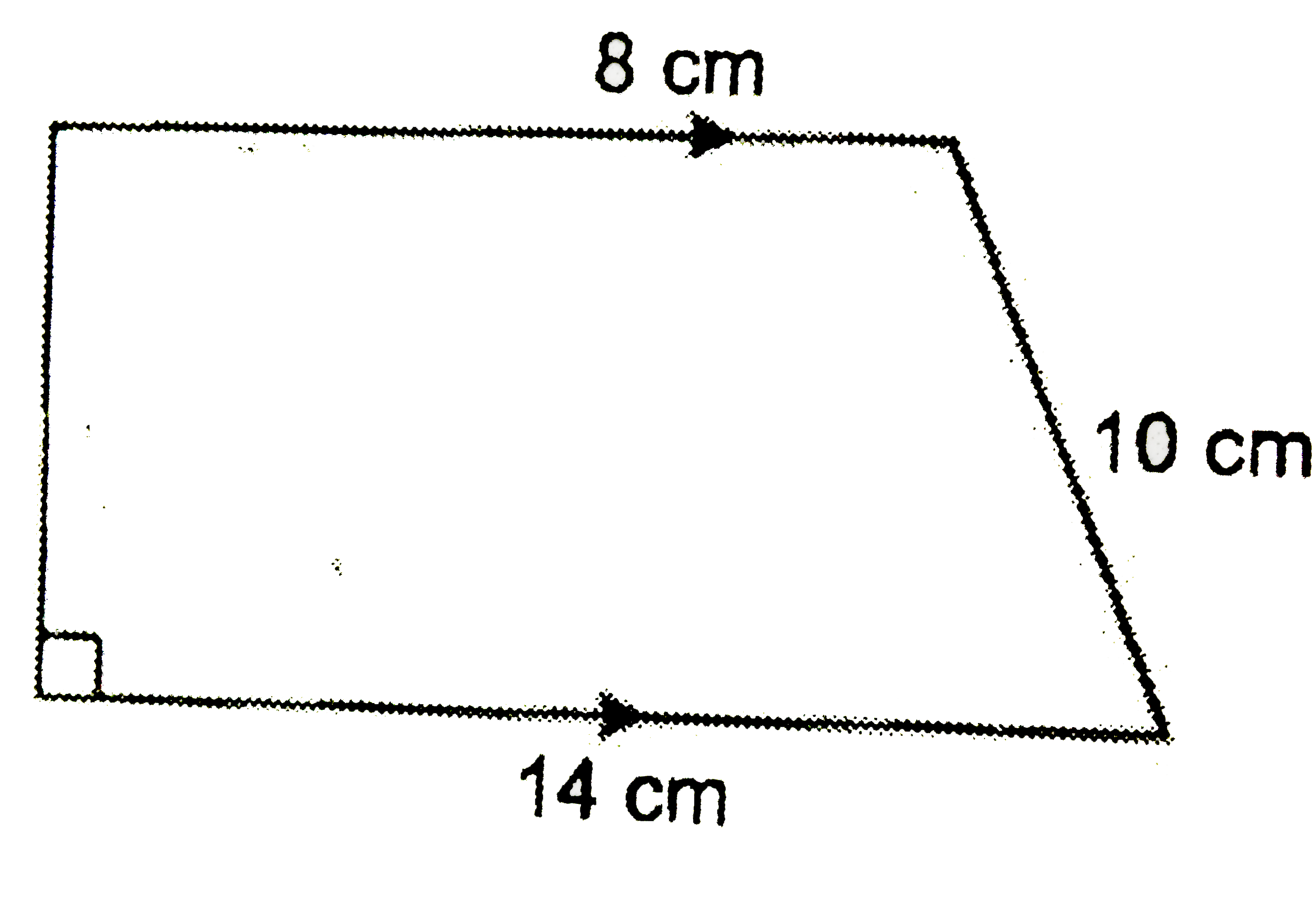
View SolutionFind the area of the trapezium given in given figure.
View SolutionFind the area of the trapezium given in adjoining figure.

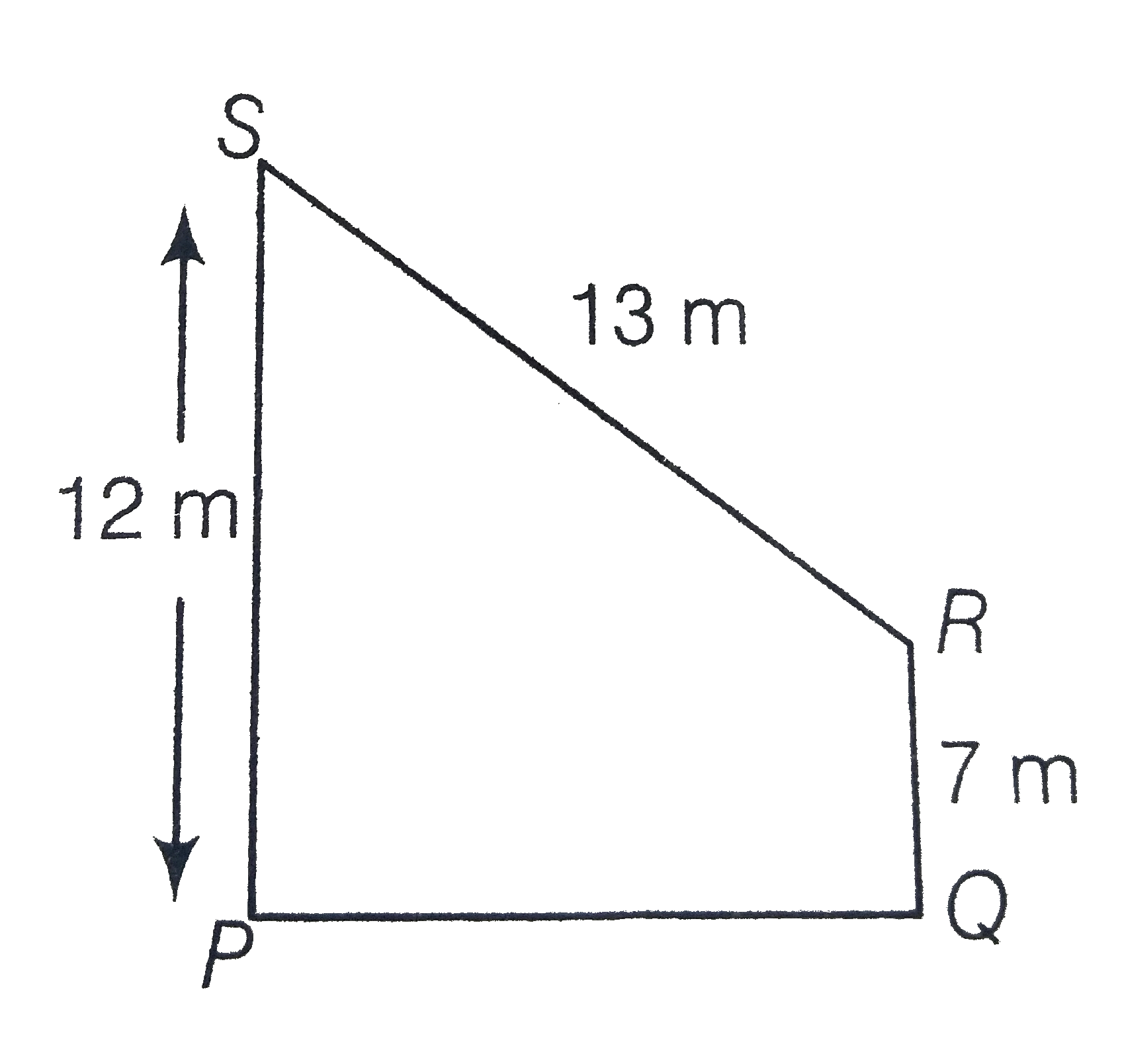
View SolutionFind the area of the trapezium PQRS with height PQ given in the figure given below
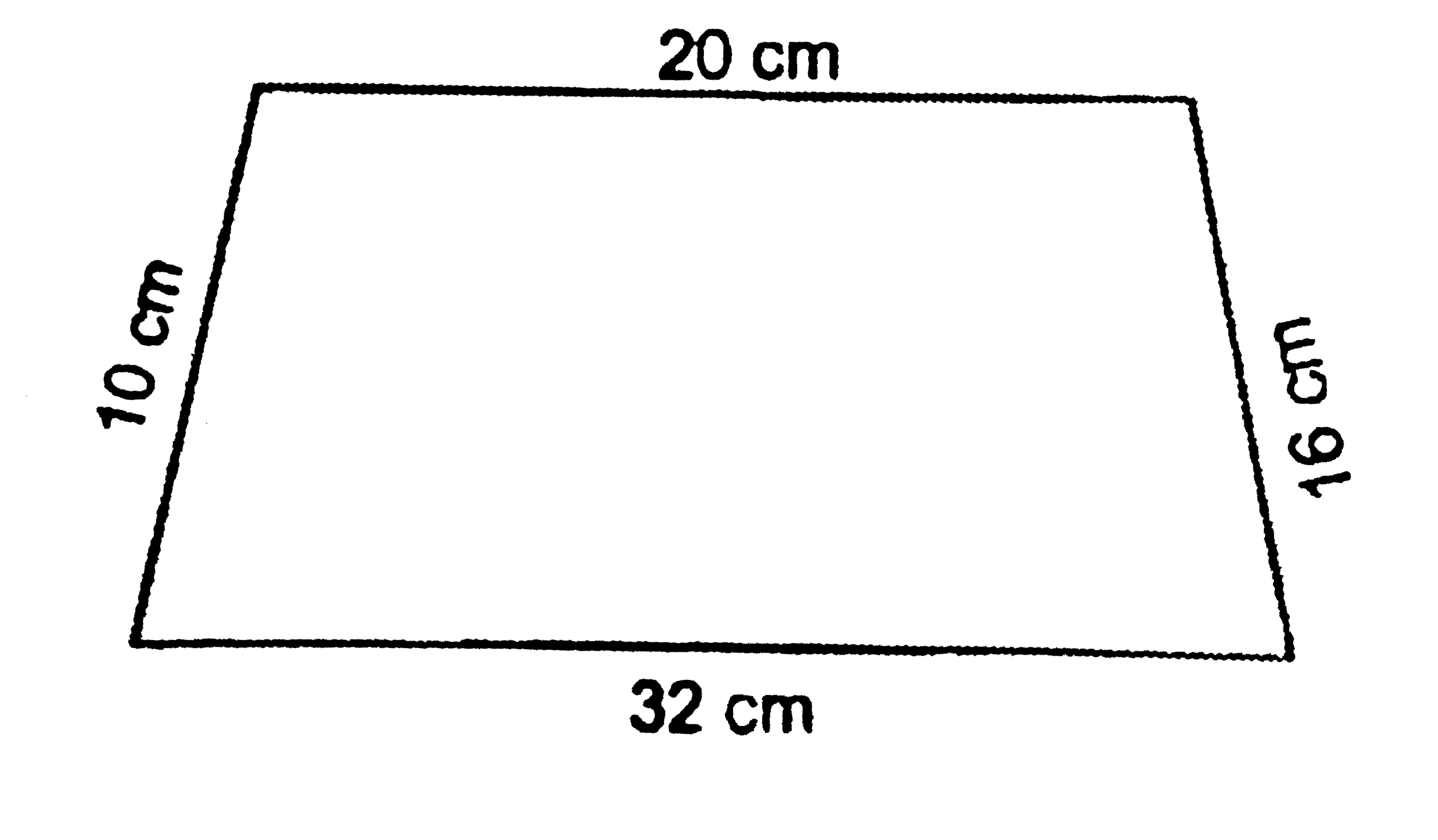
View SolutionFind the area of the given trapezium.
View SolutionWrite the products P, Q, R and S in the given reaction sequence.
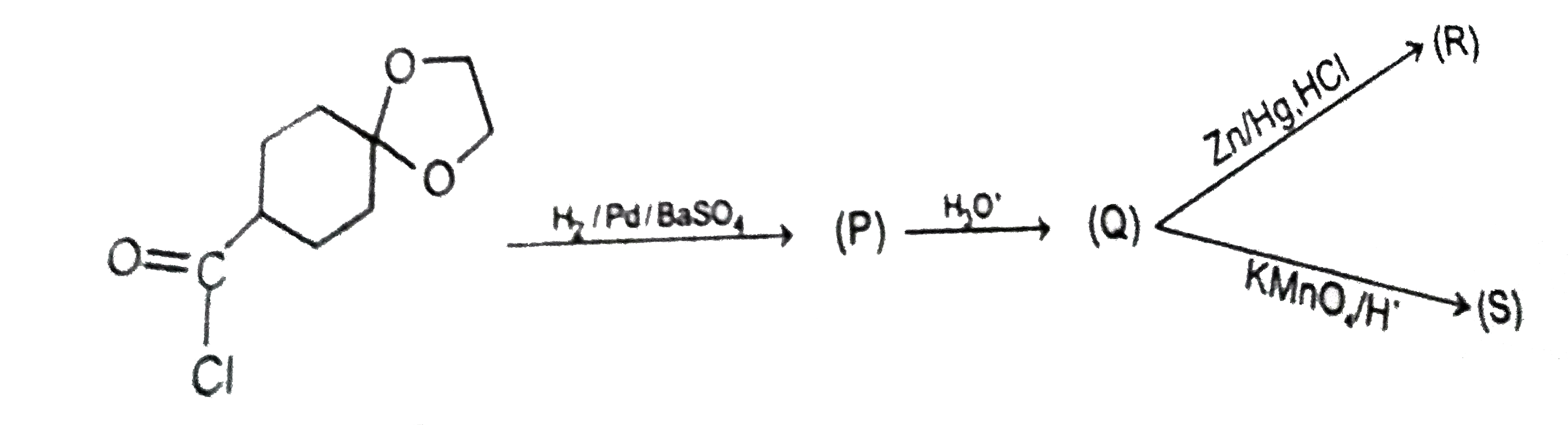
View SolutionFind the area of Figure, as the sum of the area of two trapezium and a rectangle.
View SolutionGiven below is the set up for Daniell cell. Label p, q, r, s, t in the given figure.
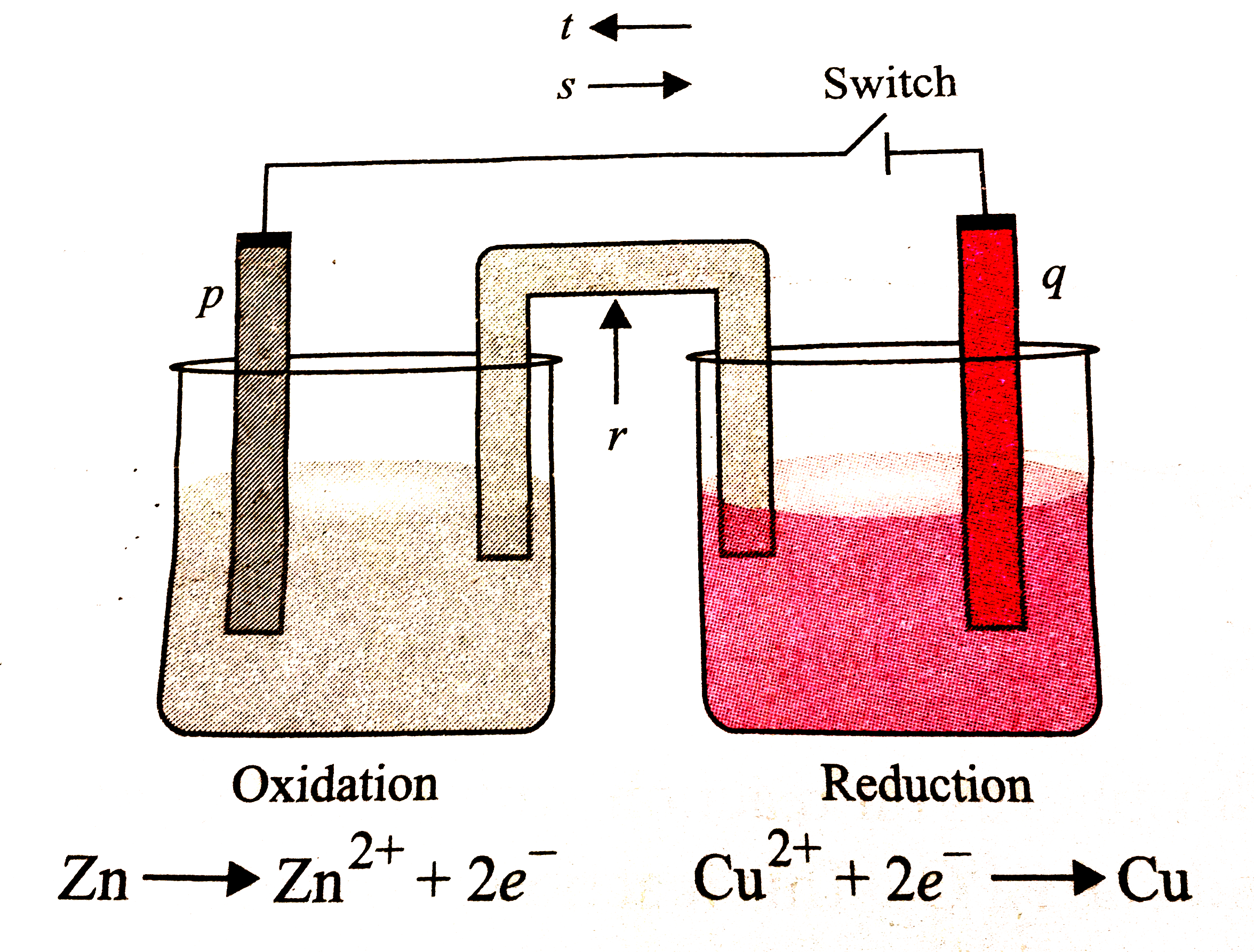
View SolutionFind the coordinates of points P, Q, R and S in Figure.
View SolutionIn Figure, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.
View Solution