Prove that any cyclic parallelogram is a rectangle.
Step by step video & image solution for Prove that any cyclic parallelogram is a rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View SolutionProve that the points (4, 5), (7, 6), (6, 3), (3, 2) are the vertices of a parallelogram. Is it a rectangle.
View SolutionIf the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
View SolutionProve that the points (3,2),(6,3),(7,6)and(4,5) are the vertices of a parallelogram. Is it a rectangle?
View Solution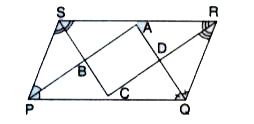
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that :
the parallelogram , inscirbed in a circle , is a rectangle.
View SolutionThe figure formed by joining the mid-point of the adjacent sides of a parallelogram is a (a)rectangle (b) parallelogram (c) rhombus (d) square
View SolutionProve that In a parallelogram, opposite side are equal
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View Solution
