A small firm manufactures items A and B. The total number of items that it can manufacture in a day is at the most 24 Item A takes on hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be 300 and that on one unit of item B be 160, how many of each type of item should be produced to maximize the profit? Solve the problem graphically
To solve the problem of maximizing profit for the small firm that manufactures items A and B, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of items A produced
- y = number of items B produced
Step 2: Formulate the Constraints
1. The total number of items produced cannot exceed 24:
x+y≤24
2. The time taken to produce items A and B must not exceed 16 hours. Since item A takes 1 hour and item B takes 0.5 hours, the constraint can be expressed as:
x+0.5y≤16
To eliminate the decimal, we can multiply the entire inequality by 2:
2x+y≤32
3. Non-negativity constraints:
x≥0,y≥0
Step 3: Formulate the Objective Function
The profit from producing items A and B can be expressed as:
Z=300x+160y
We aim to maximize Z.
Step 4: Graph the Constraints
1. Graph the first constraint x+y=24:
- When x=0, y=24 → Point (0, 24)
- When y=0, x=24 → Point (24, 0)
2. Graph the second constraint 2x+y=32:
- When x=0, y=32 → Point (0, 32)
- When y=0, 2x=32 → x=16 → Point (16, 0)
3. Plot the points on a graph and shade the feasible region defined by the inequalities.
Step 5: Identify the Corner Points
The feasible region will be bounded by the lines defined by the constraints. The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+y=24 and 2x+y=32:
- Subtract the first equation from the second:
(2x+y)−(x+y)=32−24⟹x=8
- Substitute x=8 into x+y=24:
8+y=24⟹y=16
- Corner point: (8, 16)
2. Intersection of x+y=24 and y=0:
- x+0=24⟹x=24
- Corner point: (24, 0)
3. Intersection of 2x+y=32 and y=0:
- 2x+0=32⟹x=16
- Corner point: (16, 0)
4. Intersection of x+y=24 and x=0:
- 0+y=24⟹y=24
- Corner point: (0, 24)
5. Intersection of 2x+y=32 and x=0:
- 2(0)+y=32⟹y=32
- Corner point: (0, 32) (not in feasible region)
Step 6: Calculate the Profit at Each Corner Point
1. At (0, 24):
Z=300(0)+160(24)=3840
2. At (24, 0):
Z=300(24)+160(0)=7200
3. At (8, 16):
Z=300(8)+160(16)=2400+2560=4960
4. At (16, 0):
Z=300(16)+160(0)=4800
Step 7: Determine the Maximum Profit
The maximum profit occurs at the point (24, 0) with a profit of Z=7200.
Conclusion
To maximize profit, the firm should produce:
- 24 units of item A
- 0 units of item B
Let:
- x = number of items A produced
- y = number of items B produced
1. The total number of items produced cannot exceed 24:
x+y≤24
2. The time taken to produce items A and B must not exceed 16 hours. Since item A takes 1 hour and item B takes 0.5 hours, the constraint can be expressed as:
x+0.5y≤16
To eliminate the decimal, we can multiply the entire inequality by 2:
2x+y≤32
3. Non-negativity constraints:
x≥0,y≥0
The profit from producing items A and B can be expressed as:
Z=300x+160y
We aim to maximize Z.
1. Graph the first constraint x+y=24:
- When x=0, y=24 → Point (0, 24)
- When y=0, x=24 → Point (24, 0)
- When x=0, y=32 → Point (0, 32)
- When y=0, 2x=32 → x=16 → Point (16, 0)
The feasible region will be bounded by the lines defined by the constraints. The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+y=24 and 2x+y=32:
- Subtract the first equation from the second:
(2x+y)−(x+y)=32−24⟹x=8
- Substitute x=8 into x+y=24:
8+y=24⟹y=16
- Corner point: (8, 16)
- x+0=24⟹x=24
- Corner point: (24, 0)
- 2x+0=32⟹x=16
- Corner point: (16, 0)
- 0+y=24⟹y=24
- Corner point: (0, 24)
- 2(0)+y=32⟹y=32
- Corner point: (0, 32) (not in feasible region)
1. At (0, 24):
Z=300(0)+160(24)=3840
2. At (24, 0):
Z=300(24)+160(0)=7200
3. At (8, 16):
Z=300(8)+160(16)=2400+2560=4960
4. At (16, 0):
Z=300(16)+160(0)=4800
The maximum profit occurs at the point (24, 0) with a profit of Z=7200.
To maximize profit, the firm should produce:
- 24 units of item A
- 0 units of item B
Topper's Solved these Questions
Similar Questions
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
View SolutionIf the median of 5 items is 3 and the median of another 5 items is 7. Find the median of all the 10 items taken together
View SolutionMatch the items in Column I with the relevant item in column II.
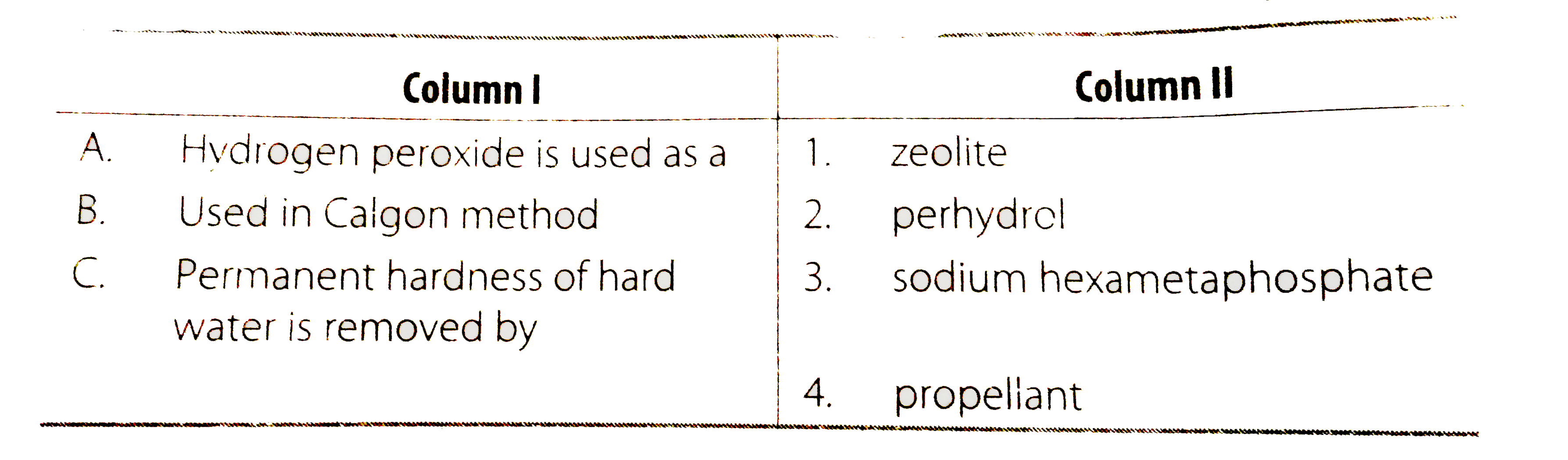
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
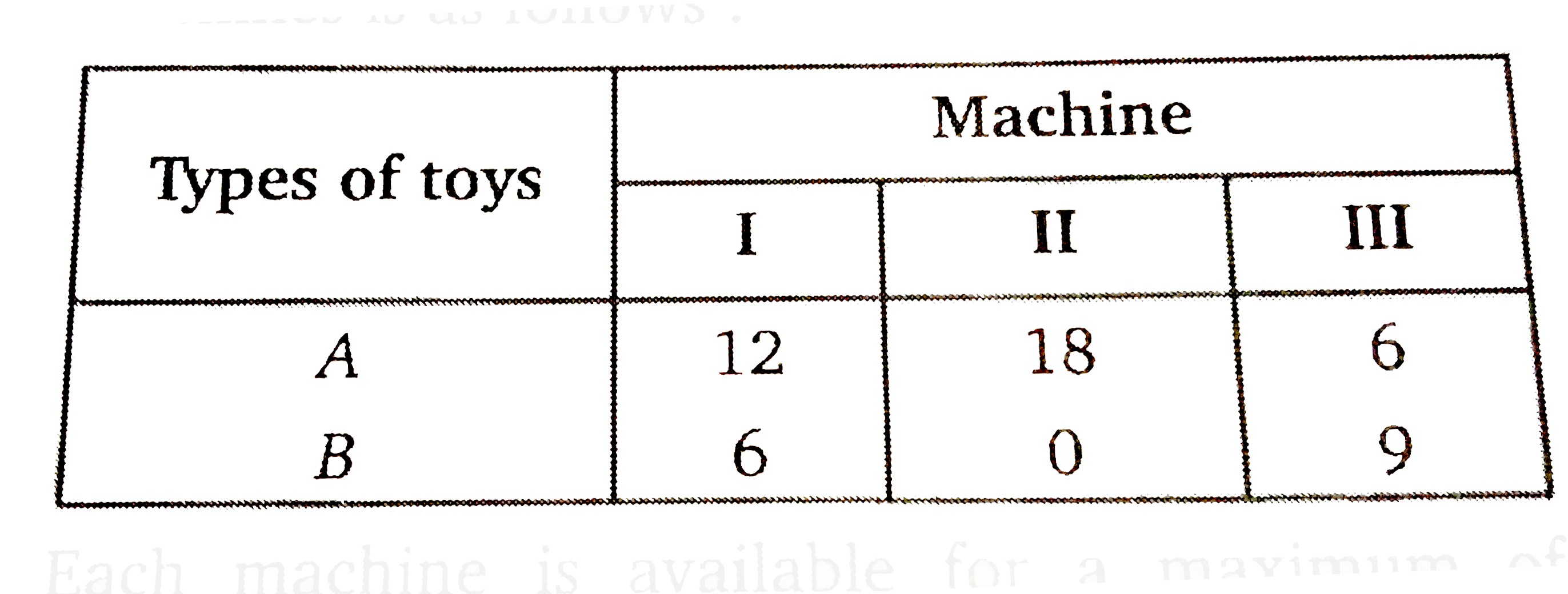 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View SolutionAn item is manufactured by three machines A, B and C. Out of hte total number of items manufactured during a specified period, 50% are manufacture on machine A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective and 3% of these produced n C are defective. All the items stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
View SolutionAn item is manufactured by three machines A, B and C. Out of the total member of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
View SolutionA company produces two types of items, and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item P requires 3 gm of gold and 1 gm of copper while that of item Q requires 1 gm of gold and 2 gm of copper. The company has 9 gm of gold and 8 gm of copper in its store. If each unit of item P makes a profit of Rs 50 and each unit of item O makes a profit of 60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit?
View SolutionThere are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?
View SolutionWhat is the total number of ways of selecting atleast one item from each of the two sets containing 6 identical items each?
View SolutionMatch the items in column I with relevant items in column II

View Solution
