Draw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): (i) OQ5 cm (ii) OP.5cm (iii) OR.5 cm
Step-by-Step Solution:
1. Draw a Circle: Begin by drawing a circle with center O and a radius of 6cm. Use a compass to ensure the circle is accurate.
Hint: Remember that the radius is the distance from the center to any point on the circle.
2. Mark Point P: Choose a point P on the circumference of the circle. Since P lies on the circle, the distance OP (from the center O to point P) is equal to the radius.
Hint: The distance OP should be exactly 6cm.
3. Mark Point Q: Now, mark a point Q inside the circle. Since Q is in the interior, the distance OQ (from the center O to point Q) must be less than 6cm.
Hint: You can choose any distance less than 6cm for OQ, such as 4cm or 5cm.
4. Mark Point R: Finally, mark a point R outside the circle. For point R, the distance OR (from the center O to point R) must be greater than 6cm.
Hint: You can choose any distance greater than 6cm for OR, such as 7cm or 8cm.
5. Rewrite Statements:
- For OQ=5cm: Since OQ is less than 6cm, we can write this as:
- OQ ≤ 5 cm (OQ can be equal to or less than 5 cm).
- For OP=5cm: Since OP is equal to the radius of the circle, we can write this as:
- OP > 5 cm (OP is greater than 5 cm).
- For OR=5cm: Since OR is greater than 6cm, we can write this as:
- OR > 5 cm (OR is greater than 5 cm).
Final Statements:
- (i) OQ ≤ 5 cm
- (ii) OP > 5 cm
- (iii) OR > 5 cm
- For OQ=5cm: Since OQ is less than 6cm, we can write this as:
- OQ ≤ 5 cm (OQ can be equal to or less than 5 cm).
- For OP=5cm: Since OP is equal to the radius of the circle, we can write this as:
- OP > 5 cm (OP is greater than 5 cm).
- For OR=5cm: Since OR is greater than 6cm, we can write this as:
- OR > 5 cm (OR is greater than 5 cm).
- (i) OQ ≤ 5 cm
- (ii) OP > 5 cm
- (iii) OR > 5 cm
Topper's Solved these Questions
Similar Questions
Mark two points, A and B on a piece of paper and join them. Measure this length. For each of the following draw a line segment CD that is: equal to the segment AB (ii) Twice AB Three times AB (iv) half AB collinear with AB and is equal to it.
View SolutionFollowing pictograph shows the number of tractors in five villages. Observe the pictograph and answer the following questions. (i) Which village has the minimum number of tractors? (ii) Which village has the maximum number of tractors? (iii) How many more tractors village C has as compared to village B. (iv) What is the total number of tractors in all the five villages?
View SolutionAP and PQ are tangents drawn from a point A to a circle with centre O and radius 9cm. If OA=15cm, then AP+AQ= (a) 12cm (b) 18cm (c) 24cm (d) 36cm
View SolutionIn Fig. 10.93, there are two concentric circles with centre O . PR and PQS are tangents to the inner circle from point plying on the outer circle. If PR=7.5cm , then PS is equal to (FIGURE) (a) 10cm (b) 12cm (c) 15cm (d) 18cm
View SolutionDraw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): OQ5 cm (ii) OP.5cm (iii) OR.5 cm
View SolutionOP……...OQ, where O is the centre of the circle, P lies on the circle and Q is in the interior of the circle.
View SolutionOP……...OR, where O is the centre of the circle, P lies on the circle and R lies in the exterior of the circle.
View SolutionFind the area of the shaded region in Fig. 12.19, if PQ=24 cm, PR=7 cm and O is the centre of the circle.
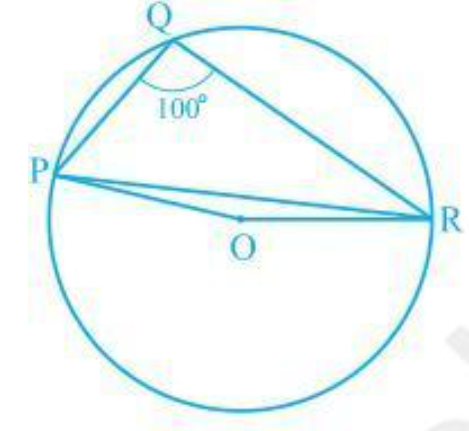
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionA line through the centre O of a circle of radius 7 cm cuts the tangent, at a point P on the circle, at Q such that PQ=24cm . Find OQ .
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ=12cm . Length PQ is
View SolutionIn Figure, there are two concentric circles with centre O . PR and PQS are tangents to the inner circle from point plying on the outer circle. If PR=7.5cm , then PS is equal to (a) 10cm (b) 12cm (c) 15cm (d) 18cm
View SolutionDraw a circle of radius 4 cm with centre O . Draw a diameter POQ . Through P or Q draw tangent to the circle.
View SolutionFind the area of the shaded region in Figure, if PQ=24cm,PR=7cm and O is the centre of the circle.
View Solution