In the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
To solve the problem step by step, we will use the properties of angles formed by parallel lines and a transversal.
1. Identify Given Information:
- We have two parallel lines AB and CD.
- A transversal PQ intersects AB at point L and CD at point M.
- We are given that ∠CMQ=60∘.
2. Find Angle 1:
- ∠CMQ and ∠1 form a linear pair (they are on a straight line).
- Therefore, ∠1+∠CMQ=180∘.
- Substitute ∠CMQ=60∘:
∠1+60∘=180∘
- Solving for ∠1:
∠1=180∘−60∘=120∘
3. Find Angle 2:
- ∠CMQ and ∠2 are vertically opposite angles.
- Therefore, ∠2=∠CMQ=60∘.
4. Find Angle 3:
- ∠1 and ∠3 are also vertically opposite angles.
- Therefore, ∠3=∠1=120∘.
5. Find Angle 4:
- ∠CMQ and ∠4 are corresponding angles.
- Therefore, ∠4=∠CMQ=60∘.
6. Find Angle 5:
- ∠1 and ∠5 are corresponding angles.
- Therefore, ∠5=∠1=120∘.
7. Find Angle 6:
- ∠2 and ∠6 are corresponding angles.
- Therefore, ∠6=∠2=60∘.
8. Find Angle 7:
- ∠3 and ∠7 are corresponding angles.
- Therefore, ∠7=∠3=120∘.
Summary of Angles:
- ∠1=120∘
- ∠2=60∘
- ∠3=120∘
- ∠4=60∘
- ∠5=120∘
- ∠6=60∘
- ∠7=120∘
- We have two parallel lines AB and CD.
- A transversal PQ intersects AB at point L and CD at point M.
- We are given that ∠CMQ=60∘.
- ∠CMQ and ∠1 form a linear pair (they are on a straight line).
- Therefore, ∠1+∠CMQ=180∘.
- Substitute ∠CMQ=60∘:
∠1+60∘=180∘
- Solving for ∠1:
∠1=180∘−60∘=120∘
- ∠CMQ and ∠2 are vertically opposite angles.
- Therefore, ∠2=∠CMQ=60∘.
- ∠1 and ∠3 are also vertically opposite angles.
- Therefore, ∠3=∠1=120∘.
- ∠CMQ and ∠4 are corresponding angles.
- Therefore, ∠4=∠CMQ=60∘.
- ∠1 and ∠5 are corresponding angles.
- Therefore, ∠5=∠1=120∘.
- ∠2 and ∠6 are corresponding angles.
- Therefore, ∠6=∠2=60∘.
- ∠3 and ∠7 are corresponding angles.
- Therefore, ∠7=∠3=120∘.
- ∠1=120∘
- ∠2=60∘
- ∠3=120∘
- ∠4=60∘
- ∠5=120∘
- ∠6=60∘
- ∠7=120∘
Similar Questions
In the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn the given figure l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn the given figure, AB||CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
View SolutionIn Fig. l, m and n are parallel lines intersected by transversal P at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn the given figure, line l || m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
View SolutionIn Figure, l, m and n are parallel lines intersected by a transversal at X, Y, and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn Fig. 51, l, m and n are parallel lines intersected by a transversal p at X,Y and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn the given figure l||mandp||q. Find the angle x,y, z
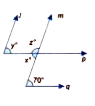
View SolutionIn the given figure, l||m||nandp||q||r. Find the angles x,y, z and t.
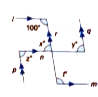
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z

View Solution