How much time is required for complete decomposition of 4 moles of water using 4 ampere?
3.86×105sec
1.93×105sec
96500sec
48250sec
The correct Answer is:B
To find the time required for the complete decomposition of 4 moles of water using a current of 4 amperes, we can follow these steps:
Step 1: Determine the number of electrons involved
The decomposition of water can be represented by the reaction:
2H2O→4H++O2+4e−
From this reaction, we see that 2 moles of water produce 4 moles of electrons (4e⁻). Therefore, for 4 moles of water:
4 moles of H2O→8H++O2+8e−
This means that 4 moles of water will produce 8 moles of electrons.
Step 2: Calculate the total charge (Q)
We know that 1 mole of electrons corresponds to 96500 coulombs (Faraday's constant). Thus, for 8 moles of electrons:
Q=8 moles×96500 C/mole=772000 C
Step 3: Use the formula relating charge, current, and time
The relationship between charge (Q), current (I), and time (t) is given by:
Q=I×t
We can rearrange this to find time:
t=QI
Step 4: Substitute the values into the equation
Substituting the values we have:
- Q=772000 C
- I=4 A
Thus,
t=772000 C4 A=193000 seconds
Step 5: Convert time into a more understandable unit (if necessary)
To convert seconds into hours, we can divide by 3600 (the number of seconds in an hour):
t=193000 seconds3600 seconds/hour≈53.61 hours
Final Answer
The time required for the complete decomposition of 4 moles of water using 4 amperes is approximately 193000 seconds or 53.61 hours.
---
The decomposition of water can be represented by the reaction:
2H2O→4H++O2+4e−
From this reaction, we see that 2 moles of water produce 4 moles of electrons (4e⁻). Therefore, for 4 moles of water:
4 moles of H2O→8H++O2+8e−
This means that 4 moles of water will produce 8 moles of electrons.
We know that 1 mole of electrons corresponds to 96500 coulombs (Faraday's constant). Thus, for 8 moles of electrons:
Q=8 moles×96500 C/mole=772000 C
The relationship between charge (Q), current (I), and time (t) is given by:
Q=I×t
We can rearrange this to find time:
t=QI
Substituting the values we have:
- Q=772000 C
- I=4 A
t=772000 C4 A=193000 seconds
To convert seconds into hours, we can divide by 3600 (the number of seconds in an hour):
t=193000 seconds3600 seconds/hour≈53.61 hours
The time required for the complete decomposition of 4 moles of water using 4 amperes is approximately 193000 seconds or 53.61 hours.
Similar Questions
Knowledge Check
How much oxygen is required for complete combustion of 560 g of ethene?
A6.4 kgB1.92 KgC2.8 kgD9.6 kg
If isobutane and n-butane are present in a gas, then how much oxygen should be required for complete combustion of 5 kg of this gas
View SolutionThe minimum number of moles of O2 required for complete combustion of 1 mole of propane and 2 moles of butane is _______.
View SolutionCalculate the time required for a current of 2 amp to decompose two moles of water.
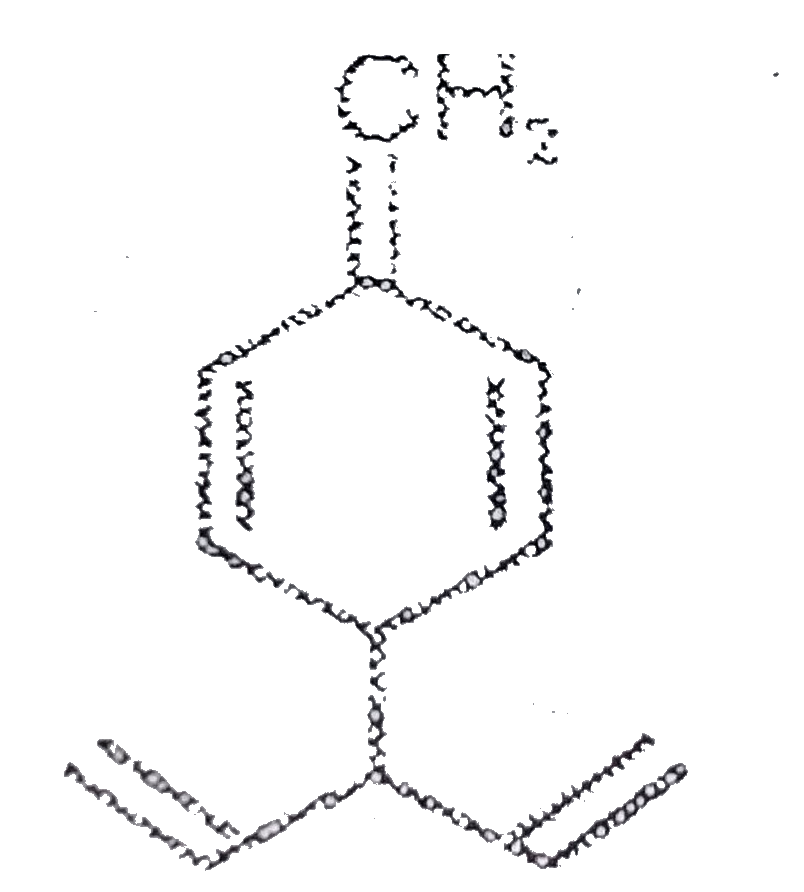
View SolutionNumber of moles of hydrogen will required for complete hydrogenation of one mole of following compounds :
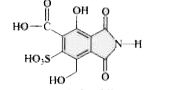
View SolutionHow many moles of NaOH would be required for complete neutralization of following compounds?
View SolutionDDT on exposure to water decomposes. How much time will it take for its 90% decomposition? (Half-life = 20 years)
View SolutionNumber of moles of oxygen required for the complete combustion of butane are
View Solution
