PtCl4.6H2Ocan exist as hydrated complex 1 molal aq.solution has depression in freezing point of 3.72∘CAssume 100% ionisation and Kf(H2O=1.86∘Cmol−1Kg) then complex is
[pt(H2O6]Cl4
[Pt(H2O)5Cl]Cl2.2H2O
[Pt(H2O)3Cl3]Cl.3H2O
[Pt(H2O)2Cl4]Cl.4H2O
The correct Answer is:c
To solve the problem, we need to determine the complex formed by PtCl4.6H2O based on the given information about the depression in freezing point of a 1 molal aqueous solution.
1. Understand the Given Information:
- Depression in freezing point (ΔTf) = 3.72 °C
- Molality (m) = 1 molal
- Freezing point depression constant (Kf) for water = 1.86 °C kg/mol
2. Use the Freezing Point Depression Formula:
The formula for freezing point depression is given by:
\(
\Delta T_f = K_f \cdot m \cdot i
\)
where:
- ΔTf = depression in freezing point
- Kf = freezing point depression constant
- m = molality of the solution
- i = Van't Hoff factor (number of particles the solute dissociates into)
3. Rearranging the Formula to Find i:
Rearranging the formula to solve for the Van't Hoff factor (i):
\(
i = \frac{\Delta T_f}{K_f \cdot m}
\)
4. Substituting the Values:
Now, substitute the known values into the equation:
\(
i = \frac{3.72}{1.86 \cdot 1}
\)
\(
i = \frac{3.72}{1.86} = 2
\)
5. Interpret the Value of i:
The value of i = 2 indicates that the complex dissociates into 2 particles in solution.
6. Identify the Possible Complexes:
Now, we need to analyze the possible complexes of PtCl4.6H2O:
- Option A: \( \text{(Pt(H}_2\text{O)}_6)^{4+} + 4 \text{Cl}^- \) → i = 5
- Option B: \( \text{(Pt(H}_2\text{O)}_5\text{Cl})^{+} + 2 \text{Cl}^- \) → i = 3
- Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \) → i = 2
- Option D: \( \text{(Pt(H}_2\text{O)}_2\text{Cl}_4)^{+} \) → i = 1
7. Conclusion:
Since we found that i = 2, the correct complex is the one that dissociates into 2 particles, which corresponds to Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \).
Final Answer:
The complex is Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \).
- Depression in freezing point (ΔTf) = 3.72 °C
- Molality (m) = 1 molal
- Freezing point depression constant (Kf) for water = 1.86 °C kg/mol
The formula for freezing point depression is given by:
\(
\Delta T_f = K_f \cdot m \cdot i
\)
where:
- ΔTf = depression in freezing point
- Kf = freezing point depression constant
- m = molality of the solution
- i = Van't Hoff factor (number of particles the solute dissociates into)
Rearranging the formula to solve for the Van't Hoff factor (i):
\(
i = \frac{\Delta T_f}{K_f \cdot m}
\)
Now, substitute the known values into the equation:
\(
i = \frac{3.72}{1.86 \cdot 1}
\)
\(
i = \frac{3.72}{1.86} = 2
\)
The value of i = 2 indicates that the complex dissociates into 2 particles in solution.
Now, we need to analyze the possible complexes of PtCl4.6H2O:
- Option A: \( \text{(Pt(H}_2\text{O)}_6)^{4+} + 4 \text{Cl}^- \) → i = 5
- Option B: \( \text{(Pt(H}_2\text{O)}_5\text{Cl})^{+} + 2 \text{Cl}^- \) → i = 3
- Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \) → i = 2
- Option D: \( \text{(Pt(H}_2\text{O)}_2\text{Cl}_4)^{+} \) → i = 1
Since we found that i = 2, the correct complex is the one that dissociates into 2 particles, which corresponds to Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \).
The complex is Option C: \( \text{(Pt(H}_2\text{O)}_3\text{Cl}_3)^{+} + \text{Cl}^- \).
Topper's Solved these Questions
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-02
26 Videos
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-03
23 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Video
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
Similar Questions
Two beaker A and B present in a closed vessel. Beaker A contains 152.4 g aqueous soulution of urea, containing 12 g of urea. Beaker B contain 196.2 g glucose solution, containing 18 g of glocose. Both solution allowed to attain the equilibrium. Determine mass % of glocose in its solution at equilibrium allowed to attain the equilibrium :
View SolutionLowering in vapour pressure is determined by Ostwald and Walker dynamic methed. It is based on the prinicipal , that when air is allowed to pass through a solvent or solution, it takes up solventvapour with it to get itself saturated at that temperature
I and II are weighted separately before and after passing dry air. Loss in mass of each set, gives the lowing of vapour pressure. The temperature of air, the solution and the solvent is kept constant.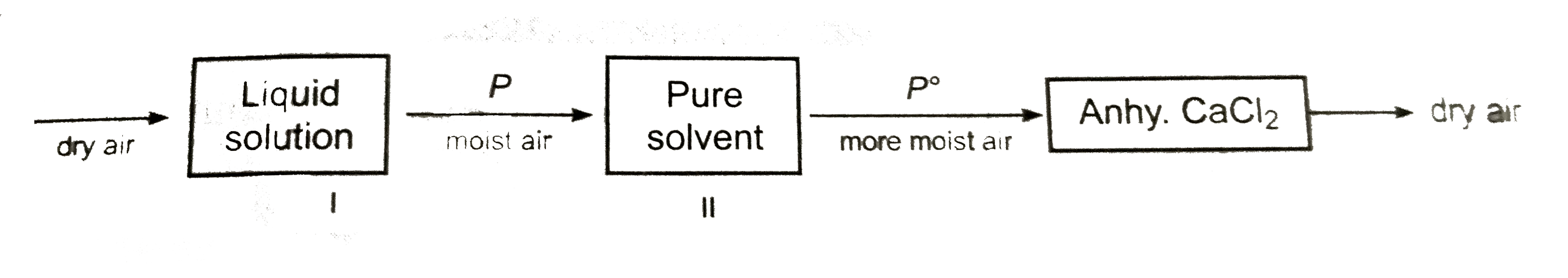
Loss in masss of solvent (wII)will be proportional to :
View SolutionColumn-I and Column-II contains fore enteries each. Entries of Column-I are to be matched with, some entries of Column-II One or more than one entries of Column-I may have the mathching with the same entries of Column-II
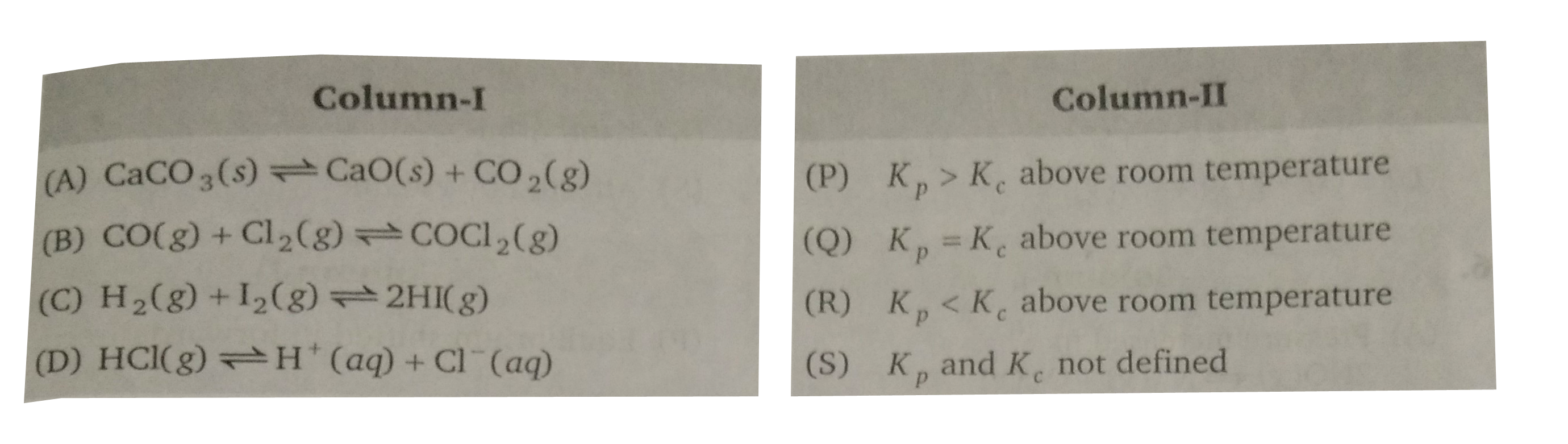
View SolutionHow many faradays are required for reduction of 1mol C6H5NO2 into C6H5NH2?
View SolutionA 0.001 molal solution of a complex represented as Pt(NH3)4Cl4 in water had freezing point depression of 0.0054∘C. Given Kf for H2O=1.86Km−1. Assuming 100% ionization of the complex, write the ionization nature and formula or complex.
View SolutionPtCl4.6H2O can exist as a hydrated complex. 1m aqueous solution has the depression in freezing point of 3.72∘. Assume 100% ionization and Kf(H2O)=1.86∘mol−1kg, then the complex is
View SolutionCompound PdCl4.6H2O is a hydrated complex, 1m aqueous solution of it has freezing point 269.28K. Assuming 100% ionization of complex, calculate the number of ions furnished by complex in the solution.
View SolutionA complex is represented as CoCl3.XNH3. Its 0.1 molal solution in aqueous solution shows ΔTf=0.558∘.(Kf for H2O is 1.86Kmolality−1) Assuming 100% ionisation of complex and co-ordination number of Co as six, calculate formula of complex.
View SolutionPtCl4.6H2Ocan exist as hydrated complex 1 molal aq.solution has depression in freezing point of 3.72∘CAssume 100% ionisation and Kf(H2O=1.86∘mol−1)kg then complex is
View SolutionPtCl_(4). 6H_(2)O can exist as hydrated complex 1 molal aq. Solution has depression in freezing point of 3.72^(@) . Assume 100% ionisation and K_(f)(H_(2)O) = 1.86^(@) mol^(-1) kg , then complex is :
View SolutionCompound PdCl_(4). 6H_(2)O is a hydrated complex, 1 molal aqueous solution of it has freezing point 269.28 K. Assuming 100% ionization of complex, calculate the molecular formula of the complex ( K_(f) for water = 1.86 K mol^(-1) )
View SolutionPtCl4⋅6H2O एक जलयोजित संकर के रूप में उपस्थित रह सकता है । इस लवण के 1 मोलल जलीय विलयन के हिमांक में 3.72∘C का अवनमन ज्ञात किया गया । माना कि लवण विलयन में 100% आयनित हो जाता है तथा H2O के लिए Kf=1.86K kg mol−1 है तब संकर का संभावित अणुसूत्र है -
View SolutionThe freezing point of 1 molal NaCl solution assuming NaCl to be 100% dissociated in water is:
View SolutionA complex is represented as CoCl_(3) . XNH_(3) . Its 0.1 molal solution in aqueous solution shows Delta T_(f) = 0.558^(circ). (K_(f) for H_(2)O is 1.86 K "molality"^(-1)) Assuming 100% ionisation of complex and co-ordination number of Co as six, calculate formula of complex.
View SolutionA 0.001 molal solution of a complex represented as Pt(NH3)4Cl4 in water had freezing point depression of 0.0054∘C. Given Kf for H2O=1.86Km−1. Assuming 100% ionization of the complex, write the ionization nature and formula or complex.
View Solution

