Two particles of de-broglie wavelength λx and λy are moving in opposite direction. Find debroglie wavelength after perfectly inelastic collision:
λxλy∣∣λx−λy∣∣
2λxλyλx−λy
λxλ2yλy−λx
λy−λx
The correct Answer is:A
To find the de Broglie wavelength after a perfectly inelastic collision between two particles moving in opposite directions, we can follow these steps:
Step 1: Understand the de Broglie wavelength and momentum
The de Broglie wavelength (λ) of a particle is related to its momentum (p) by the formula:
p=hλ
where h is Planck's constant.
Step 2: Define the momenta of the two particles
Let the two particles have de Broglie wavelengths λx and λy. The momenta of the two particles can be expressed as:
px=hλx(for particle with wavelength λx)
py=hλy(for particle with wavelength λy)
Since the particles are moving in opposite directions, we can assign the momentum of the first particle as positive and the second particle as negative:
px+(−py)=hλx−hλy
Step 3: Apply conservation of momentum
In a perfectly inelastic collision, the two particles stick together and move with a common momentum after the collision. Let λ be the de Broglie wavelength of the combined particle after the collision. The total momentum after the collision can be expressed as:
ptotal=hλ
By conservation of momentum, we have:
hλx−hλy=hλ
Step 4: Simplify the equation
We can factor out h from the equation:
1λx−1λy=1λ
This can be rewritten as:
1λ=λy−λxλxλy
Step 5: Solve for λ
Taking the reciprocal of both sides gives us:
λ=λxλyλy−λx
To ensure that the denominator is positive, we can express it as:
λ=λxλy|λy−λx|
Final Answer
Thus, the de Broglie wavelength after the perfectly inelastic collision is:
λ=λxλy|λy−λx|
---
The de Broglie wavelength (λ) of a particle is related to its momentum (p) by the formula:
p=hλ
where h is Planck's constant.
Let the two particles have de Broglie wavelengths λx and λy. The momenta of the two particles can be expressed as:
px=hλx(for particle with wavelength λx)
py=hλy(for particle with wavelength λy)
Since the particles are moving in opposite directions, we can assign the momentum of the first particle as positive and the second particle as negative:
px+(−py)=hλx−hλy
In a perfectly inelastic collision, the two particles stick together and move with a common momentum after the collision. Let λ be the de Broglie wavelength of the combined particle after the collision. The total momentum after the collision can be expressed as:
ptotal=hλ
By conservation of momentum, we have:
hλx−hλy=hλ
We can factor out h from the equation:
1λx−1λy=1λ
This can be rewritten as:
1λ=λy−λxλxλy
Taking the reciprocal of both sides gives us:
λ=λxλyλy−λx
To ensure that the denominator is positive, we can express it as:
λ=λxλy|λy−λx|
Thus, the de Broglie wavelength after the perfectly inelastic collision is:
λ=λxλy|λy−λx|
Topper's Solved these Questions
Similar Questions
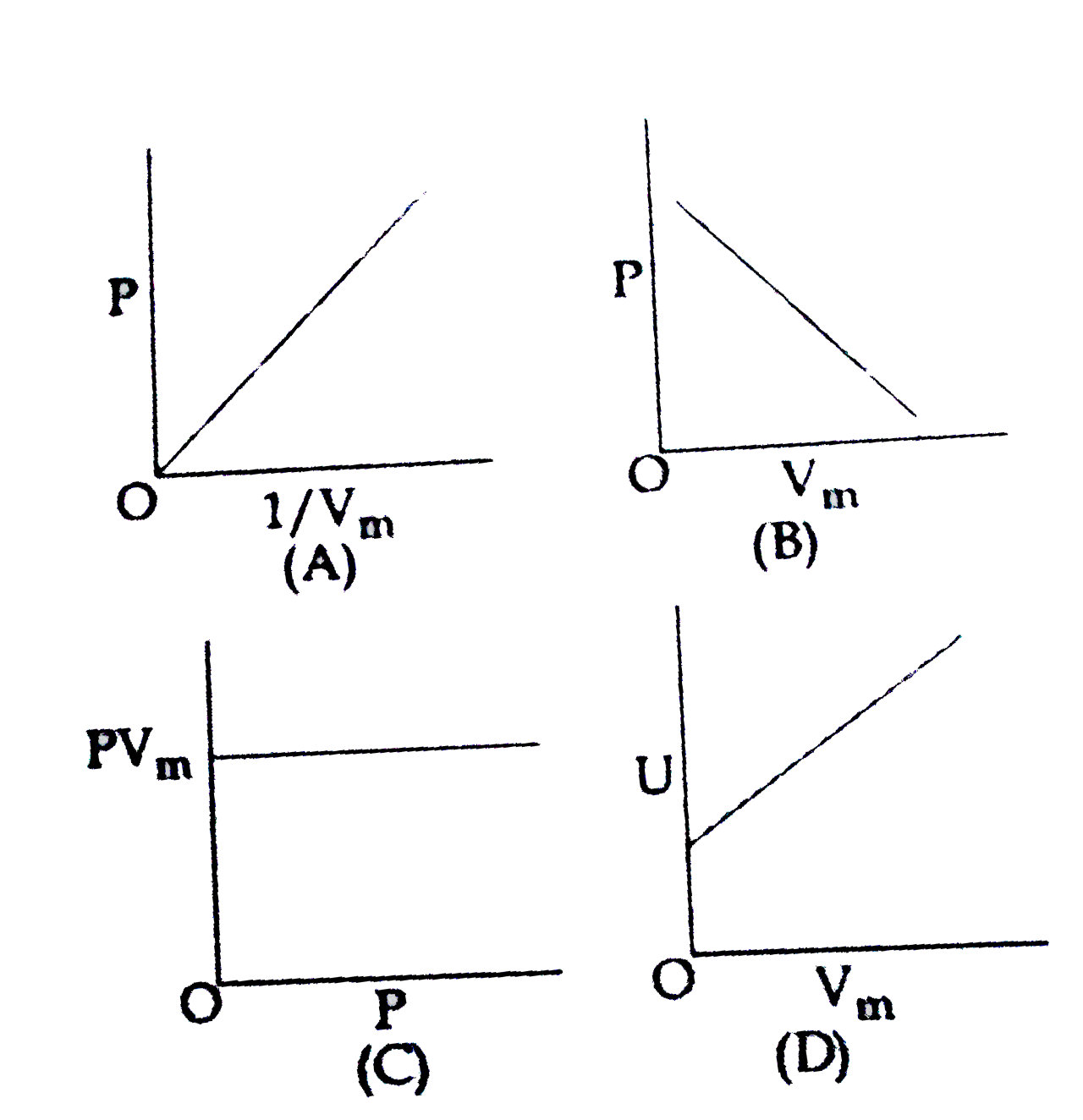
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionTwo particles of de-broglie wavelength lamda_(x) and lamda_(y) are moving in opposite direction. Find debroglie wavelength after perfectly inelastic collision:
View SolutionIf alpha particle, proton and electron move with the same momentum, them their respective de Broglie wavelengths lamda_(alpha),lamda_(p),lamda_(e) are related as
View SolutionThe energy of a photon is equal to the kinetic energy of a proton. If λ1 is the de-Broglie wavelength of a proton, λ2 the wavelength associated with the proton and if the energy of the photon is E, then (λ1/λ2) is proportional to
View SolutionA particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de Broglie wavelength of the particle varies cyclically between two values lamda_(1), lamda_(2) " with " lamda_(1) gt lamda_(2) . Which of the following statements are true?
View SolutionA particle A of mass m and initial velocity v collides with a particle of B of mass m/2 which is at rest. The collision is head-on and elastic. The ratio of the de Broglie wavelengths lamda_(A) "to" lamda_(B) after collision is
View SolutionTwo particles having de-Broglie wavelengths lambda_(1) and lambda_(2) , while moving along mutually perpendicular directions, undergo perfectly inelastic collision. The de-Broglie wavelength lambda , of the final particle is
View SolutionA particle ‘P’ is formed due to a completely inelastic collision of particles ‘x’ and ‘y’ having de-Broglie wavelength lambda_(x) and lambda_(y) respectively. If x and y were moving in opposite directions, then the de-Broglie wavelength of ‘P’ is:
View SolutionTwo particles move at right angle to each other.Their de Broglie wavelengths are lambda_(1) and lambda_(2) respectively.The particles suffer perfectly inelastic collision.The de Broglie wavelength lambda of the final particle is given by :
View SolutionAn α− particle and a proton are accelerated from rest by a potential difference of 100 V. After this, their de Broglie wavelengths are and λa and λp respectively. The ratio λpλa to the nearest integer, is ...............
View SolutionA particle 'P' is formed due to a completely inelastic collision of particles 'x' and 'y' having de-Broglie wavelength 'λx' and 'λy respectively. If x and y were moving in opposite directions, then the de-Broglie wavelength 'P' is :
View SolutionThe energy of a photon is equal to the kinetic energy of a proton. If λ1 is the de Broglie wavelength of a proton, λ2 the wavelength associated with the photon, and if the energy of the photon is E, then (λ1/λ2) is proportional to
View SolutionIf alpha particle, proton and electron move with the same momentum, them their respective de Broglie wavelengths lamda_(alpha),lamda_(p),lamda_(e) are related as
View Solution

