Equation of motion for a particle performing damped harmonic oscillation is given as x=e−0.1tcos(10πt+ϕ). The time when amplitude will half of the initial is :
27
4
1
7
The correct Answer is:D
To solve the problem, we need to determine the time when the amplitude of a damped harmonic oscillator is half of its initial value. The equation of motion given is:
x(t)=e−0.1tcos(10πt+ϕ)
1. Identify the Initial Amplitude:
The initial amplitude A0 can be identified from the equation. The amplitude of the oscillation is given by the exponential term:
A(t)=A0e−0.1t
Here, A0 is the initial amplitude at t=0.
2. Set Up the Equation for Half Amplitude:
We want to find the time t when the amplitude is half of the initial amplitude:
A(t)=A02
Substituting the expression for amplitude:
A0e−0.1t=A02
3. Cancel A0:
Since A0 is non-zero, we can divide both sides of the equation by A0:
e−0.1t=12
4. Take the Natural Logarithm:
To solve for t, we take the natural logarithm of both sides:
ln(e−0.1t)=ln(12)
This simplifies to:
−0.1t=ln(12)
5. Solve for t:
Rearranging the equation gives:
t=ln(12)−0.1
We know that ln(12)=−ln(2), so:
t=−ln(2)−0.1=ln(2)0.1
6. Calculate t:
The value of ln(2) is approximately 0.693:
t=0.6930.1=6.93 seconds
7. Round to the Nearest Whole Number:
Rounding 6.93 seconds gives us approximately 7 seconds.
Final Answer:
The time when the amplitude will be half of the initial amplitude is approximately 7 seconds.
The initial amplitude A0 can be identified from the equation. The amplitude of the oscillation is given by the exponential term:
A(t)=A0e−0.1t
Here, A0 is the initial amplitude at t=0.
We want to find the time t when the amplitude is half of the initial amplitude:
A(t)=A02
Substituting the expression for amplitude:
A0e−0.1t=A02
Since A0 is non-zero, we can divide both sides of the equation by A0:
e−0.1t=12
To solve for t, we take the natural logarithm of both sides:
ln(e−0.1t)=ln(12)
This simplifies to:
−0.1t=ln(12)
Rearranging the equation gives:
t=ln(12)−0.1
We know that ln(12)=−ln(2), so:
t=−ln(2)−0.1=ln(2)0.1
The value of ln(2) is approximately 0.693:
t=0.6930.1=6.93 seconds
Rounding 6.93 seconds gives us approximately 7 seconds.
The time when the amplitude will be half of the initial amplitude is approximately 7 seconds.
Topper's Solved these Questions
Similar Questions
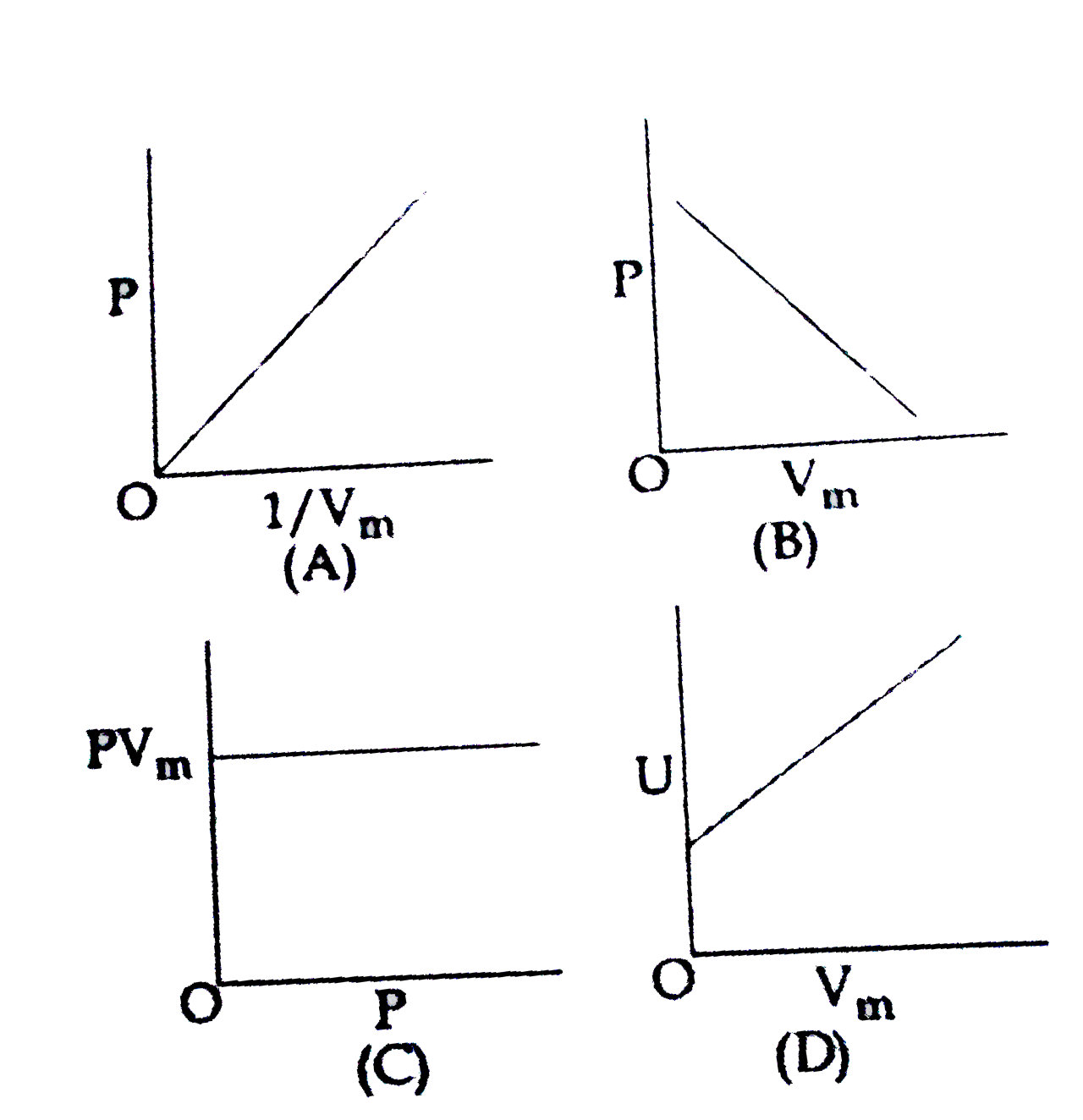
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionA particle is performing damped oscillation with frequency 5Hz. After every 10 oscillations its amplitude becmoes half. Find time from beginning after which the amplitude becomes 1/1000 of its initial amplitude :
View SolutionEquation of motion for a particle performing damped harmonic oscillation is given as x=e−1tcos(10πt+ϕ). The time when amplitude will half of the initial is :
View SolutionIn a damped harmonic oscillator, periodic oscillations have ………. amplitude.
View SolutionA simple harmonic motion of amplitude A has a time period T. The acceleration of the oscillator when its displacement is half the amplitude is
View Solutionएक अवमन्दित आवर्ती दोलक का विस्थापन निम्न है, x(t)=e−0.1tcos[10πt+ϕ], यहाँ t सेकण्ड में है। इसके दोलन आयाम को अपने आरम्भिक मान से आधा होने में लगे समय का सन्निकट मान होगा-
View SolutionFor a damped oscillation of a particle, show that time taken for the amplitude to drop to half of its initial value =2mln(2)b, where b is a damping constant.
View SolutionThe equation describing the motion of a simple harmonic oscillator along the X axis is given as x = A cos (omega t + phi) . If at time t = 0, the oscillator is at x = 0 and moving in the negative x direction, then the phase angle phi is
View SolutionThe displacement of a damped harmonic oscillator is given by x(t)=e^(-0.1t)cos(10pit+phi) . Here t is in seconds The time taken for its amplitude of vibration to drop to half of its initial is close to :
View SolutionA oscillator of mass 100g executes damped oscillation. When it complete 100 oscillations its amplitude of oscillation becomes half to its original amplitude. If time period is 2s, then find the value of damping coefficient.
View SolutionA particle executes simple harmonic motion with an amplitude A. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude form the equilibrium position is………..
View SolutionA particle is performing damped oscillation with frequency 5Hz . After every 10 oscillations its amplitude becmoes half. Find time from beginning after which the amplitude becomes 1//1000 of its initial amplitude :
View SolutionThe displacement of a damped harmonic oscillator is given by
x(t)−e−0.1tcos(10πt+φ).Here t is in seconds.
The time taken for its amplitude of vibration to drop to half of its initial value is close to :
View Solution

