A particle of mass 'm' is moving with speed '2v' and collides with a mass '2m' moving with speed 'v' in the same direction. After collision, the first mass is stopped completely while the second one splits into two particles each of mass 'm' which move at angle 45∘ with respect to the original direction. The speed of each of the moving particle will be
√2v
2√2v
v/(2√2)
v/√2
The correct Answer is:D
To solve the problem, we will use the principle of conservation of momentum. Let's break down the solution step by step.
Step 1: Understand the Initial Conditions
We have two particles:
- Particle A (mass = m) moving with speed = 2v.
- Particle B (mass = 2m) moving with speed = v in the same direction.
Step 2: Calculate Initial Momentum
The initial momentum of the system can be calculated as follows:
- Momentum of Particle A = mass × velocity = m × 2v = 2mv.
- Momentum of Particle B = mass × velocity = 2m × v = 2mv.
Total initial momentum (P_initial) = Momentum of A + Momentum of B
Pinitial=2mv+2mv=4mv.
Step 3: Analyze the Final Conditions
After the collision:
- Particle A comes to a complete stop (final velocity = 0).
- Particle B splits into two particles, each of mass m, moving at an angle of 45 degrees with respect to the original direction.
Let the speed of each of the two new particles be v′.
Step 4: Calculate Final Momentum
The final momentum can be analyzed in two components (x-direction and y-direction).
X-Direction:
- The momentum of each of the two particles in the x-direction is m⋅v′⋅cos(45∘)=m⋅v′⋅1√2.
- Since there are two particles, the total momentum in the x-direction after the collision is:
Pfinal, x=2(m⋅v′⋅1√2)=2mv′√2=√2mv′.
Y-Direction:
- The momentum of one particle in the y-direction is m⋅v′⋅sin(45∘)=m⋅v′⋅1√2.
- One particle moves in the positive y-direction and the other in the negative y-direction, so their momenta cancel each other out:
Pfinal, y=m⋅v′⋅1√2−m⋅v′⋅1√2=0.
Step 5: Apply Conservation of Momentum
Since there is no external force acting on the system, the total momentum before the collision must equal the total momentum after the collision.
In the x-direction:
Pinitial=Pfinal, x.
4mv=√2mv′.
Step 6: Solve for v′
Dividing both sides by m (assuming m≠0):
4v=√2v′.
Now, solve for v′:
v′=4v√2=2√2v.
Final Answer
The speed of each of the moving particles after the collision is:
v′=2√2v.
We have two particles:
- Particle A (mass = m) moving with speed = 2v.
- Particle B (mass = 2m) moving with speed = v in the same direction.
The initial momentum of the system can be calculated as follows:
- Momentum of Particle A = mass × velocity = m × 2v = 2mv.
- Momentum of Particle B = mass × velocity = 2m × v = 2mv.
Pinitial=2mv+2mv=4mv.
After the collision:
- Particle A comes to a complete stop (final velocity = 0).
- Particle B splits into two particles, each of mass m, moving at an angle of 45 degrees with respect to the original direction.
The final momentum can be analyzed in two components (x-direction and y-direction).
- The momentum of each of the two particles in the x-direction is m⋅v′⋅cos(45∘)=m⋅v′⋅1√2.
- Since there are two particles, the total momentum in the x-direction after the collision is:
Pfinal, x=2(m⋅v′⋅1√2)=2mv′√2=√2mv′.
- The momentum of one particle in the y-direction is m⋅v′⋅sin(45∘)=m⋅v′⋅1√2.
- One particle moves in the positive y-direction and the other in the negative y-direction, so their momenta cancel each other out:
Pfinal, y=m⋅v′⋅1√2−m⋅v′⋅1√2=0.
Since there is no external force acting on the system, the total momentum before the collision must equal the total momentum after the collision.
Pinitial=Pfinal, x.
4mv=√2mv′.
Dividing both sides by m (assuming m≠0):
4v=√2v′.
Now, solve for v′:
v′=4v√2=2√2v.
The speed of each of the moving particles after the collision is:
v′=2√2v.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
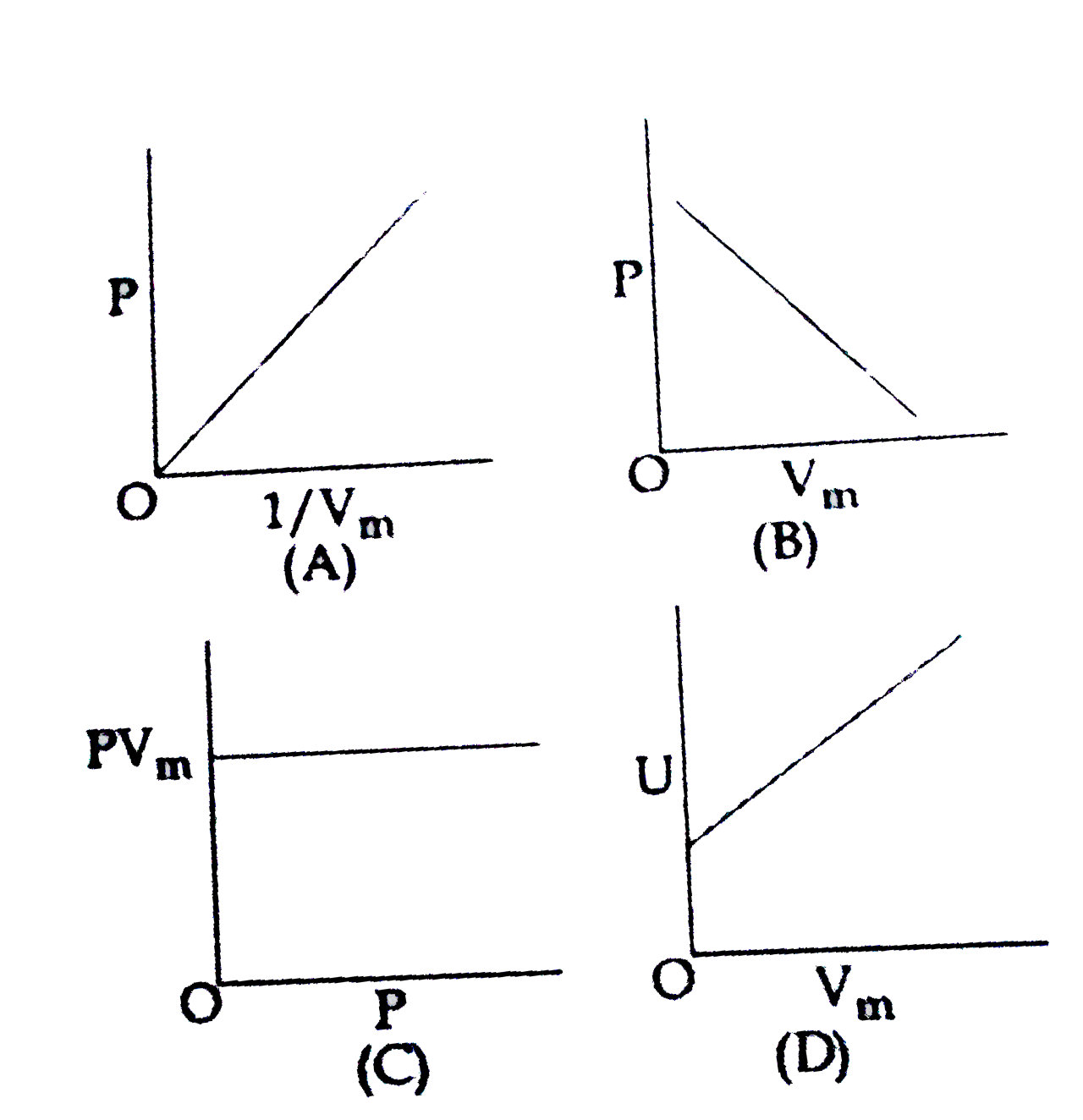
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View SolutionA particle of mass m moving eastward with a speed v collides with another particle of the same mass moving coalesce on collision. The new particle of mass 2 m will move in the north - easterly direction with a velocity
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then Speed of the particles after collision
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then Find the angle with the horizontal to which the particles move after collision.
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
View SolutionA particle of mass ‘m’ is moving with speed ‘2v’ and collides with a mass ‘2m’ moving with speed ‘v’ in the same direction. After collision, the first mass is stopped completely while the second one splits into two particles each of mass ‘m’, which move at angle 45∘ with respect to the original direction. The speed of each of the moving particle will be:
View Solutionद्रव्यमान 'm' का एक कण चाल '2v' से जाते हुए एक द्रव्यमान '2m' के कण जो इसी दिशा में चाल 'v' से जा रहा है , से संघट्ट करता है । संघट्ट के बाद पहला कण स्थिर अवस्था में आ जाता है तथा दूसरा कण ही द्रव्यमान 'm' के दो कणो में विभाजित हो जाता है । ये दोनों कण आरंभिक दिशा से 45∘ के कोण पर जाते है । ये दोनों कण आरंभिक दिशा से के कोण पर जाते है । प्रत्येक चलायमान कण की गति का मान होगा -
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. if the collision is perfectly inelastic , the percentage loss in the energy during the collision is close to
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View SolutionA particle of m mass moving at a speed v towards the east collides with another particle of the same mass moving at the same speed v towards the north. After the collision both particles stick together. It will move in a new particle of mass 2 m, moving in the northeast direction?
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View Solution
