Moment of inertia of a body about a given axis is 1.5kgm2. Intially the body is at rest. In order to produce a rotational kinetic energy iof 1200 J, the angular acceleration of 20 rad/s2 must be applied about the axis for a duration of
2.5 s
2s
5s
3s
The correct Answer is:B
To solve the problem, we need to find the time duration for which an angular acceleration of 20 rad/s² must be applied to a body with a moment of inertia of 1.5 kg m² in order to produce a rotational kinetic energy of 1200 J.
1. Identify Given Values:
- Moment of inertia, I=1.5kg m2
- Initial angular velocity, ω0=0rad/s (the body is at rest)
- Rotational kinetic energy, K=1200J
- Angular acceleration, α=20rad/s2
2. Use the Formula for Rotational Kinetic Energy:
The formula for rotational kinetic energy is given by:
K=12Iω2
Rearranging this formula to find ω:
ω2=2KI
3. Substituting the Values:
Substitute the known values into the equation:
ω2=2×1200J1.5kg m2
ω2=24001.5=1600
4. Calculate Angular Velocity:
Taking the square root to find ω:
ω=√1600=40rad/s
5. Use the Angular Motion Equation:
The relationship between angular velocity, initial angular velocity, angular acceleration, and time is given by:
ω=ω0+αt
Since ω0=0:
ω=αt
6. Substituting Known Values:
Substitute ω=40rad/s and α=20rad/s2:
40=20t
7. Solve for Time t:
Rearranging gives:
t=4020=2s
Final Answer:
The time duration for which the angular acceleration must be applied is t=2s.
---
- Moment of inertia, I=1.5kg m2
- Initial angular velocity, ω0=0rad/s (the body is at rest)
- Rotational kinetic energy, K=1200J
- Angular acceleration, α=20rad/s2
The formula for rotational kinetic energy is given by:
K=12Iω2
Rearranging this formula to find ω:
ω2=2KI
Substitute the known values into the equation:
ω2=2×1200J1.5kg m2
ω2=24001.5=1600
Taking the square root to find ω:
ω=√1600=40rad/s
The relationship between angular velocity, initial angular velocity, angular acceleration, and time is given by:
ω=ω0+αt
Since ω0=0:
ω=αt
Substitute ω=40rad/s and α=20rad/s2:
40=20t
Rearranging gives:
t=4020=2s
The time duration for which the angular acceleration must be applied is t=2s.
Topper's Solved these Questions
Similar Questions
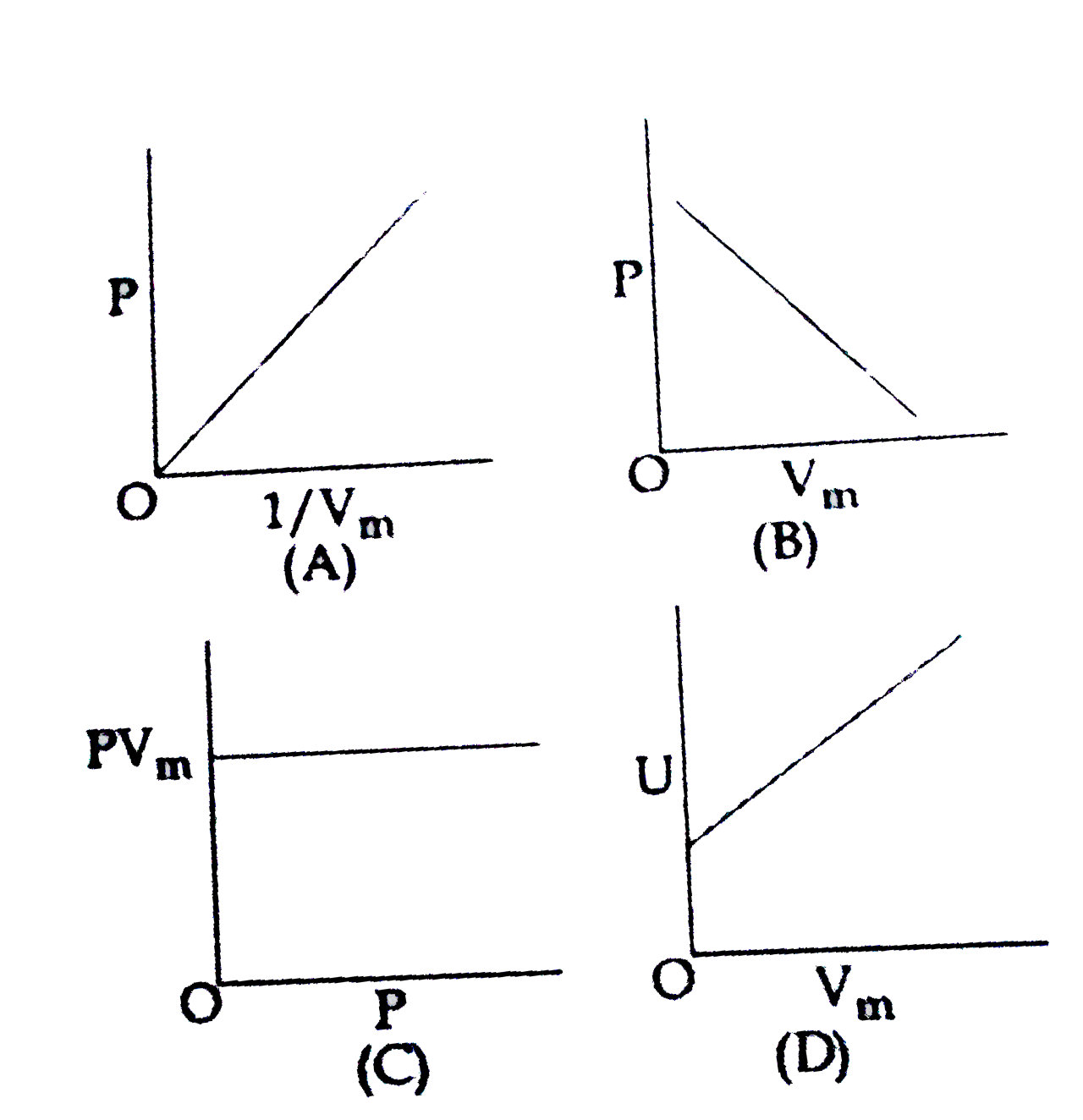
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionThe moment of inertia of a body about a given axis is 1.2kgm2. Initially, the body is at rest. In order to produce a rotational KE of 1500j, for how much duration, an acceleration of 25rads−2 must be applied about that axis ?
View SolutionThe moment of inertia of a body about a given axis is 1.2kgm2. Initially, the body is at rest. In order to produce a rotational KE of 1500J, for how much duration, an acceleration of 25rads−2 must be applied about that axis ?
View SolutionThe moment of inertia of the body about an axis is 1.2 kg m^(2) . Initially the body is at rest. In order to produce a rotational kinetic energy of 1500J, an angualr acceleration of 25 rad/s^(2) must be applied about the axis for the duration of
View SolutionIf the kinetic energy of rotation of a body about an axis is 9 J and the moment of inertia is 2 kg m2, then the angular velocity of the body about the axis of rotation in rad/s is
View SolutionThe moment of inertia of a body about a given axis is 3.6 kg m2. Initially, the body is at rest. In order to produce a rotational K.E. of 800 J, an acceleration of 15 rad s must be applied about that axis for
View SolutionMoment of inertia of a body about a given axis is 1.5 kg m^(2) . Initially the body is at rest. In order to produce a rotational kinetic energy of 1200 J, the angular acceleration of 20 rad//s^(2) must be applied about the axis for a duration of _________ (in sec).
View SolutionThe moment of inertia of a body about a given axis is 12 kg.m^(2) . Initially, the body is at rest. In order to produce a rotational kinetic energy of 15000J, an angular acceleration of 10 rads^(-2) must be applied about that axis for a duration of
View SolutionThe M.I. of a body is 1.2 kg m2. Initially the body is at rest. In order to produce a rotational kinetic energy of 1500 J an angular acceleration of 25 rad s−2 must be applied about the axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 1.2 kg m^2 . Initially, the body is at rest. In order to produce a rotational kinetic energy of 6000 joule, an angular acceleration of 25 rad/ s^2 must be applied about that axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 1.2 kg m2. · Initially, the body is at rest. In order to produce a rotational kinetic energy of 1500 J, an angular acceleration of 25 rad/s2 must be applied about that axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 2.4kg–m2. To produce a rotational kinetic energy of 750 J, an angular acceleration of 5 rad/s2 must be applied about that axis for
View SolutionThe M.I. of a body is 1.2 kg m2. Initially the body is at rest. In order to produce a rotational kinetic energy of 1500 J an angular acceleration of 25 rad s−2 must be applied about the axis for a duration os
View Solution

