The relative uncertainty in the period of a satellite orbiting around the earth is 10−2 . If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
3×10−2
6×10−2
10−2
2×10−2
The correct Answer is:D
To solve the problem, we need to find the relative uncertainty in the mass of the Earth based on the given relative uncertainty in the period of a satellite orbiting the Earth.
1. Understanding the Formula for the Period of a Satellite:
The period T of a satellite in orbit is given by the formula:
T=2π√R3GM
where R is the radius of the orbit, G is the gravitational constant, and M is the mass of the Earth.
2. Squaring the Period Equation:
To simplify our calculations, we can square both sides of the equation:
T2=4π2R3GM
3. Taking the Logarithm:
We take the natural logarithm of both sides to facilitate the calculation of uncertainties:
ln(T2)=ln(4π2R3GM)
This can be rewritten using logarithmic properties:
2ln(T)=ln(4π2)+3ln(R)−ln(G)−ln(M)
4. Applying Uncertainty Relations:
The relative uncertainty in a product or quotient can be expressed as the sum of the relative uncertainties:
ΔTT=12ΔMM+3ΔRR+ΔGG
Given that the relative uncertainty in the radius R is negligible (ΔR/R≈0) and G is a constant with no uncertainty, we can simplify this to:
ΔTT=12ΔMM
5. Substituting the Given Values:
We know from the problem statement that the relative uncertainty in the period ΔTT=10−2:
10−2=12ΔMM
6. Solving for the Relative Uncertainty in Mass:
Rearranging the equation gives:
ΔMM=2×10−2=2×10−2
Thus, the relative uncertainty in the mass of the Earth is:
ΔMM=2×10−2
Final Answer:
The relative uncertainty in the mass of the Earth is 2×10−2.
The period T of a satellite in orbit is given by the formula:
T=2π√R3GM
where R is the radius of the orbit, G is the gravitational constant, and M is the mass of the Earth.
To simplify our calculations, we can square both sides of the equation:
T2=4π2R3GM
We take the natural logarithm of both sides to facilitate the calculation of uncertainties:
ln(T2)=ln(4π2R3GM)
This can be rewritten using logarithmic properties:
2ln(T)=ln(4π2)+3ln(R)−ln(G)−ln(M)
The relative uncertainty in a product or quotient can be expressed as the sum of the relative uncertainties:
ΔTT=12ΔMM+3ΔRR+ΔGG
Given that the relative uncertainty in the radius R is negligible (ΔR/R≈0) and G is a constant with no uncertainty, we can simplify this to:
ΔTT=12ΔMM
We know from the problem statement that the relative uncertainty in the period ΔTT=10−2:
10−2=12ΔMM
Rearranging the equation gives:
ΔMM=2×10−2=2×10−2
ΔMM=2×10−2
The relative uncertainty in the mass of the Earth is 2×10−2.
Topper's Solved these Questions
Similar Questions
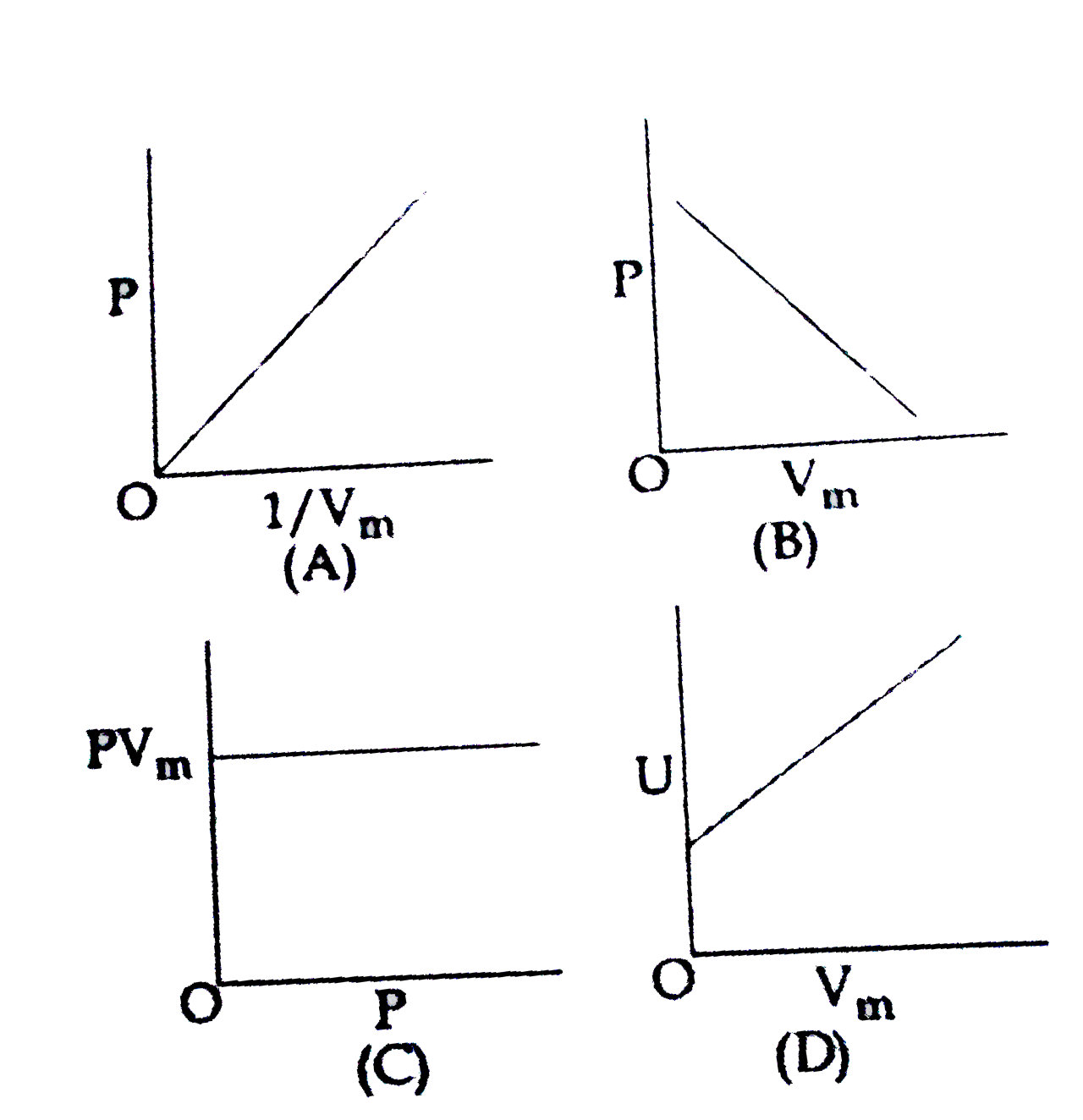
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionThe mean radius of the orbit of a satellite is 4 times as great as that of the parking orbit of the earth. Then its period of revolution around the earth is
View SolutionA satellite is orbiting around earth with its orbit radius 16 times as great as that of parking satellite. What is the period of this satellite.
View SolutionThe relative uncertainty in the period of a satellite orbiting around the earth is 10^(-2) . If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
View SolutionA satellite is orbiting around the earth at a mean radius of 16 times that of the geostationary orbit. What is the period of the satellite ?
View SolutionVelocity of geostationary satellite relative to the earth is
View Solutionm द्रव्यमान का एक उपग्रह पृथ्वी ( द्रव्यमान M ) के चारों ओर r त्रिज्या की कक्ष में घूम रहा है । कक्ष के केंद्र के परितः उपग्रह का कोणीय संवेग होगा -
View SolutionAn earth satellite X is revolving around earth in an orbit whose radius is one - fourth the radius of orbit of a communication satellite . Time period of revolution of X is .
View SolutionThe mass satellite m orbits the earth in a circular orbit of radius r. Determine the angular momentum of the satellite relative to the center of the cell.
View SolutionA satellite is orbiting the earth in an elliptical orbit. The rate of change of area (relative to time) passed by the straight line connecting the earth and the satellite is proportional to which of the following?
View Solutionएक उपग्रह जिसका m है r त्रिज्या की वृत्तीय कक्षा में प्रथ्वी के अनुदिश परिक्रमण कर रहा है | इसके कक्षा केन्द्र के सापेक्ष इसका कोणीय संवेग होगा | (M = पृथ्वी का द्रव्यमान, G = सार्वत्रिक गुरुत्वाकर्षण नियतांक)
View Solutionm द्रव्यमान का एक उपग्रह एकसमान कोणीय वेग से पृथ्वी की परिक्रमा कर रहा है | यदि कक्षा की त्रिज्या R0 तथा प्रथ्वी का द्रव्यमान M है, तो उपग्रह का पृथ्वी के केन्द्र के सापेक्ष कोणीय संवेग है
View SolutionObtain an expression for the period of a satellite in a circular orbit round the earth
OR
Show that the square of the period of revolution of satellite is directly proportional to the cube of the orbital radius.
OR
Show that period of the satellite revolving around the earth depends upon mass of the earth
View Solution

