Let C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
1
12
14
2
The correct Answer is:C
To solve the problem, we need to determine the ratio t1t2, where t1 is the time taken for the energy stored in a capacitor to reduce to half its initial value, and t2 is the time taken for the charge to reduce to one-fourth its initial value.
1. Initial Energy of the Capacitor:
The initial energy E0 stored in the capacitor is given by:
E0=Q202C
where Q0 is the initial charge and C is the capacitance.
2. Energy at Time t1:
At time t1, the energy is half of the initial energy:
E(t1)=E02=Q22C
Setting these equal gives:
Q22C=Q204C
Simplifying this, we find:
Q2=Q202⟹Q=Q0√2
3. Charge Decay Formula:
The charge Q at time t is given by:
Q=Q0e−tRC
Substituting Q=Q0√2 at t=t1:
Q0√2=Q0e−t1RC
Dividing both sides by Q0:
1√2=e−t1RC
4. Taking Logarithms:
Taking the natural logarithm of both sides:
ln(1√2)=−t1RC
This simplifies to:
−12ln(2)=−t1RC⟹t1=RC⋅12ln(2)
5. Charge at Time t2:
Now, we consider the time t2 when the charge reduces to one-fourth of its initial value:
Q(t2)=Q04
Using the charge decay formula:
Q04=Q0e−t2RC
Dividing both sides by Q0:
14=e−t2RC
6. Taking Logarithms Again:
Taking the natural logarithm:
ln(14)=−t2RC
This simplifies to:
−2ln(2)=−t2RC⟹t2=RC⋅2ln(2)
7. Finding the Ratio t1t2:
Now we can find the ratio:
t1t2=RC⋅12ln(2)RC⋅2ln(2)=122=14
Conclusion:
Thus, the ratio t1t2 is 14.
The initial energy E0 stored in the capacitor is given by:
E0=Q202C
where Q0 is the initial charge and C is the capacitance.
At time t1, the energy is half of the initial energy:
E(t1)=E02=Q22C
Setting these equal gives:
Q22C=Q204C
Simplifying this, we find:
Q2=Q202⟹Q=Q0√2
The charge Q at time t is given by:
Q=Q0e−tRC
Substituting Q=Q0√2 at t=t1:
Q0√2=Q0e−t1RC
Dividing both sides by Q0:
1√2=e−t1RC
Taking the natural logarithm of both sides:
ln(1√2)=−t1RC
This simplifies to:
−12ln(2)=−t1RC⟹t1=RC⋅12ln(2)
Now, we consider the time t2 when the charge reduces to one-fourth of its initial value:
Q(t2)=Q04
Using the charge decay formula:
Q04=Q0e−t2RC
Dividing both sides by Q0:
14=e−t2RC
Taking the natural logarithm:
ln(14)=−t2RC
This simplifies to:
−2ln(2)=−t2RC⟹t2=RC⋅2ln(2)
Now we can find the ratio:
t1t2=RC⋅12ln(2)RC⋅2ln(2)=122=14
Thus, the ratio t1t2 is 14.
Similar Questions
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View SolutionHow many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit ?
View SolutionHow many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit ?
View SolutionA simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
View SolutionA parallel plate capacitor of 1μF capacity is discharging thorugh a resistor. If its energy reduces to half in one second. The value of resistance will be
View SolutionWhen the uncharged capacitor is charged through a resistor 'R' by a battery of emf 'epsilon’' as shown, the time taken to get charge that is 50% of the equilibrium value would be
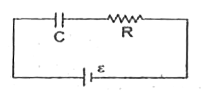
View SolutionA charged capacitor is allowed to dischare through a resistor by closing the key at the instant t=0. At the instant t=(ln4)μs, the reading of the ammeter falls half the initial vaslue. The resistance of the ammeter is equal to
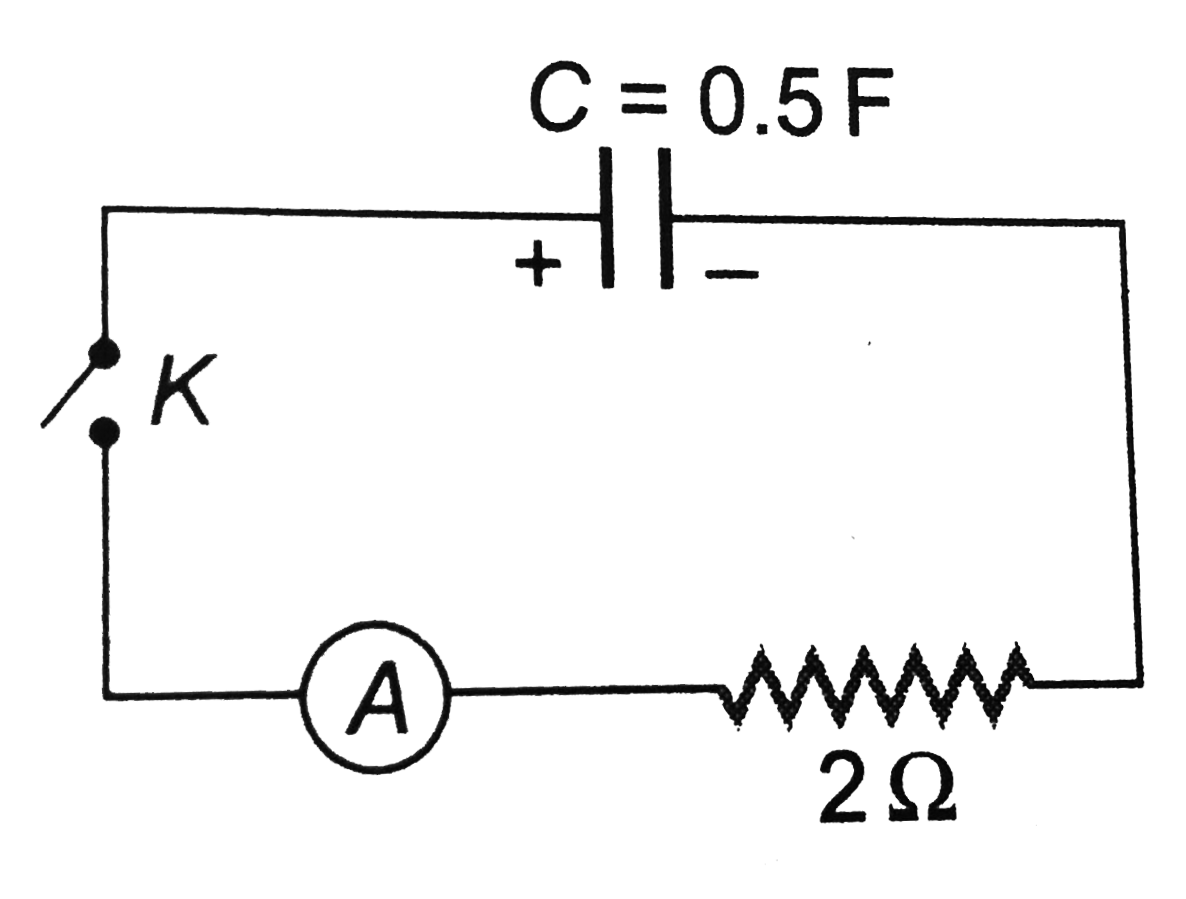
View SolutionA charged capacitor is allowed to discharged through a resistor 2Ω by closing the switch K at the t=0. At time t=2μs, the reading of the falls half of its initial value. The resistance of ammeter is equal to

View SolutionIf initial concentration is reduced to 1/4th in a zero order reaction , the time taken for half the reaction to complete
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View Solution

