There are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

σ2ε0[(1−√32)ˆy−12ˆx]
σ2ε0[(1+√32)ˆy−12ˆx]
σ2ε0[(1−√32)ˆy+12ˆx]
σ2ε0[(1+√32)ˆy+12ˆx]
The correct Answer is:A
Step by step video & image solution for There are two infinite plane sheets each having uniform surface charge density +sigma C//m ^(2) They are inclined to each other at an angle 30^(@ )as shown in the figure. Electric field at any arbitrary point P is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
There are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

View SolutionTwo infinite sheets of unifrom charge density +σand−σ are parallel to each other as shown in the figure. Electric field at the
View SolutionTwo infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
View SolutionFigure represent an infinite sheet of charge of surface charge density σ . You have to find electric field Intensity at P due to this infinite charge.
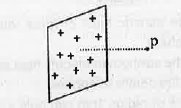 br Find electric field intensity at P due to this sheet
br Find electric field intensity at P due to this sheet
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View SolutionTwo infinite nonconducting sheets of uniform charge density (+δ) and (−δ) are parallel to each other as shown. Electric field at the
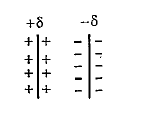
View SolutionTwo uniform infinite planes of charge having charge densities (+sigma) and (-sigma) intersect at right angle. The magnitude of electric field at any position in the space is
View Solution
