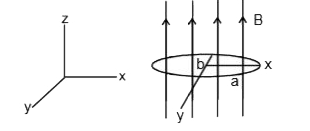
An ellipse with semi major axis 'a' semi minor 'b' revolving in uniform magnetic field'B'. Find value of average of joule heating (resistance =R)
To find the average Joule heating produced by an ellipse with semi-major axis 'a' and semi-minor axis 'b' revolving in a uniform magnetic field 'B', we can follow these steps:
Step 1: Understand the Concept of EMF
When a conductor moves in a magnetic field, an electromotive force (EMF) is induced. The average Joule heating can be expressed in terms of the current generated by this EMF.
Step 2: Expression for Average Joule Heating
The average Joule heating H can be expressed as:
H=I2RT
where I is the current, R is the resistance, and T is the time duration.
Step 3: Find the Expression for EMF
The induced EMF (E) in the ellipse can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ is the magnetic flux. The magnetic flux through the ellipse is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ellipse and θ is the angle between the magnetic field and the normal to the area.
Step 4: Area of the Ellipse
The area A of the ellipse is:
A=πab
Step 5: Substitute the Area into the EMF Expression
Substituting the area into the flux expression gives:
Φ=B⋅(πab)⋅cos(θ)
Step 6: Differentiate to Find EMF
Since the ellipse is rotating with angular velocity ω, we have:
θ=ωt
Thus, the EMF becomes:
E=−ddt(B⋅πab⋅cos(ωt))=B⋅πab⋅ωsin(ωt)
Step 7: Current as a Function of Time
The current I can be expressed in terms of the EMF:
I=ER=B⋅πab⋅ωsin(ωt)R
Step 8: Substitute Current into Joule Heating Expression
Substituting I into the Joule heating expression gives:
H=∫T0I2Rdt=∫T0(B⋅πab⋅ωsin(ωt)R)2Rdt
Step 9: Simplify the Expression
This simplifies to:
H=(B⋅πab⋅ω)2R∫T0sin2(ωt)dt
Step 10: Evaluate the Integral
The integral ∫T0sin2(ωt)dt can be evaluated. The average value of sin2(ωt) over one complete cycle is T2.
Step 11: Final Expression for Average Joule Heating
Thus, the average Joule heating is:
H=(B⋅πab⋅ω)2R⋅T2
Substituting T with 2πω (the period of rotation), we find:
H=(B⋅πab⋅ω)2R⋅πω
This simplifies to:
H=π2a2b2B2ω22R
Final Result
The average Joule heating produced by the revolving ellipse is:
H=π2a2b2B2ω22R
When a conductor moves in a magnetic field, an electromotive force (EMF) is induced. The average Joule heating can be expressed in terms of the current generated by this EMF.
The average Joule heating H can be expressed as:
H=I2RT
where I is the current, R is the resistance, and T is the time duration.
The induced EMF (E) in the ellipse can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ is the magnetic flux. The magnetic flux through the ellipse is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ellipse and θ is the angle between the magnetic field and the normal to the area.
The area A of the ellipse is:
A=πab
Substituting the area into the flux expression gives:
Φ=B⋅(πab)⋅cos(θ)
Since the ellipse is rotating with angular velocity ω, we have:
θ=ωt
Thus, the EMF becomes:
E=−ddt(B⋅πab⋅cos(ωt))=B⋅πab⋅ωsin(ωt)
The current I can be expressed in terms of the EMF:
I=ER=B⋅πab⋅ωsin(ωt)R
Substituting I into the Joule heating expression gives:
H=∫T0I2Rdt=∫T0(B⋅πab⋅ωsin(ωt)R)2Rdt
This simplifies to:
H=(B⋅πab⋅ω)2R∫T0sin2(ωt)dt
The integral ∫T0sin2(ωt)dt can be evaluated. The average value of sin2(ωt) over one complete cycle is T2.
Thus, the average Joule heating is:
H=(B⋅πab⋅ω)2R⋅T2
Substituting T with 2πω (the period of rotation), we find:
H=(B⋅πab⋅ω)2R⋅πω
This simplifies to:
H=π2a2b2B2ω22R
The average Joule heating produced by the revolving ellipse is:
H=π2a2b2B2ω22R
Similar Questions
An elliptical loop having resistance R, of semi major axis a, and semi minor axis b is placed in a magnetic field as shown in the figure. If the loop is rotated about the x-axis with angular frequency ω, the average power loss in the loop due to Joule heating is :
View SolutionA coil of radius R rotating about a diametrical axis with angular velocity 'omega' in a uniform magnetic field B. Find the value of maximum voltage developed R = 10cm B = 5 x 10^(-5) T. For half rotation it takes a time of 0.2 sec
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
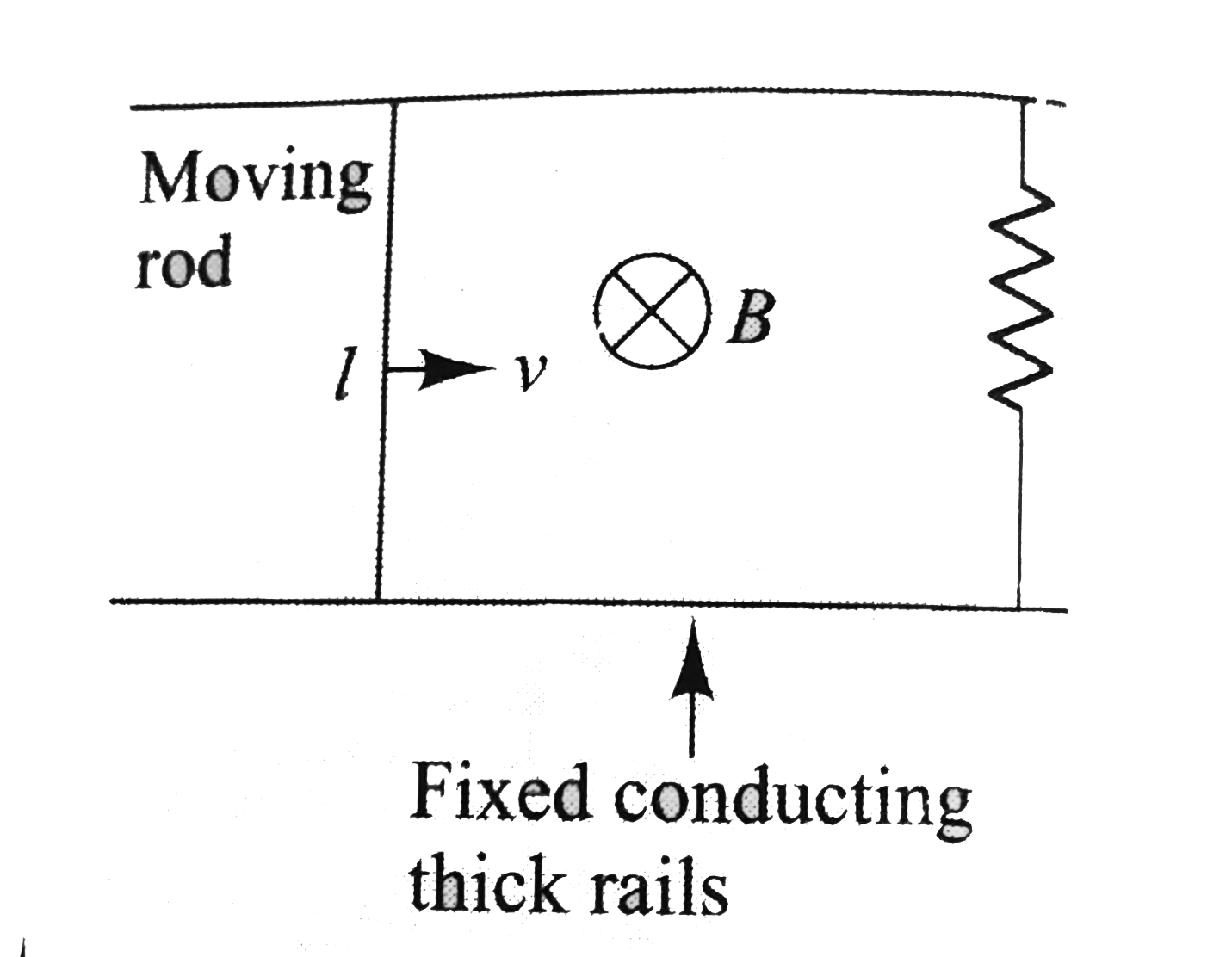
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
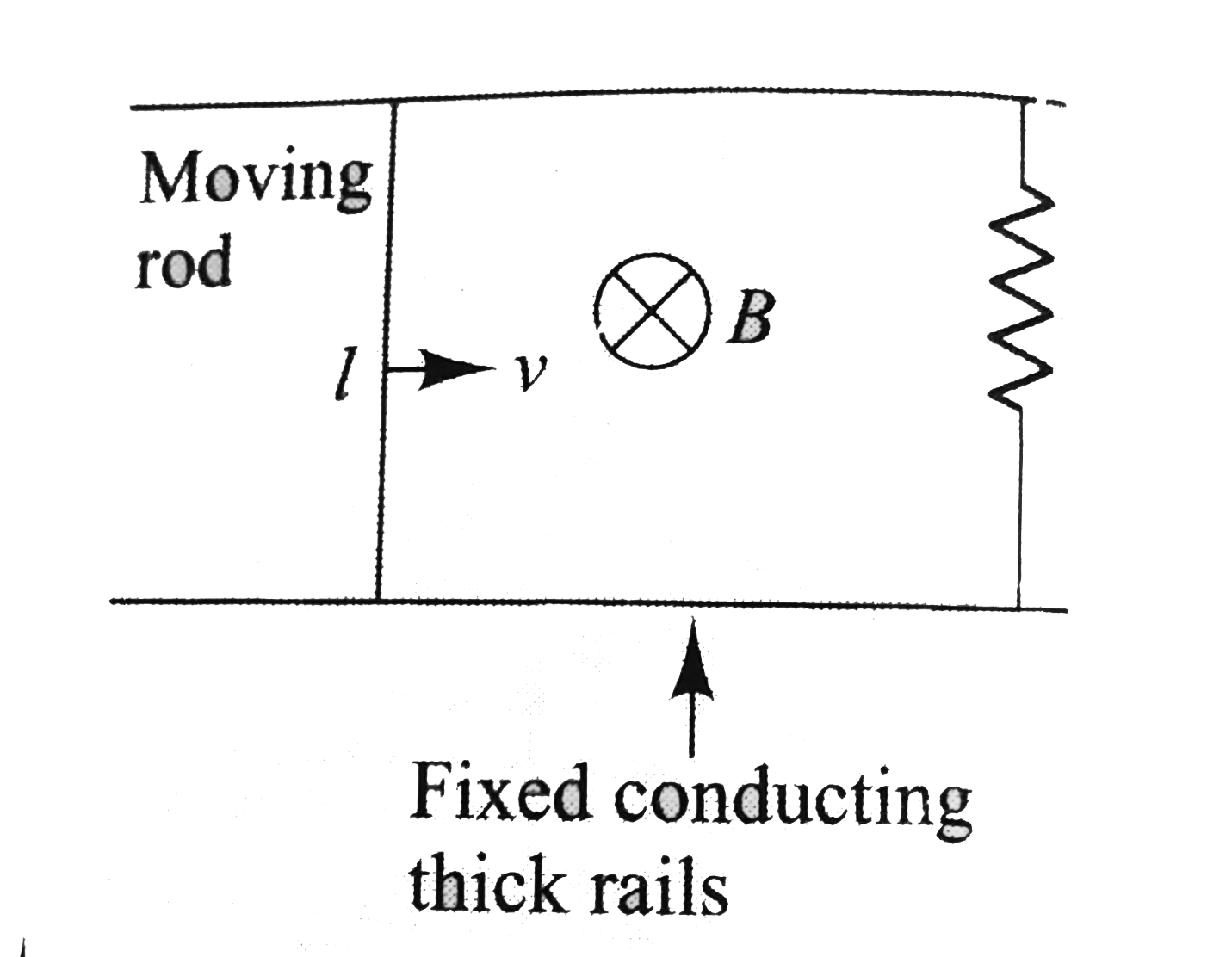
View SolutionThe major axis of an ellipse is twice its minor axis. Find its eccentricity.
View SolutionIf the length of the latus rectum of an ellipse with major axis along x-axis and centre at origin is 20 units, distance between foci is equal to length of minor axis, then find the equation of the ellipse.
View SolutionA negatively charged particle enters in a semi-infinite uniform magnetic field vecB, directed out the plane of paper as shown in the figure. Through what angle it is is deviated when it leaves the magnetic field?
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionPoint 'O' is the centre of the ellipse with major axis AB & minor axis CD. Point F is one focus of the ellipse. If OF = 6 & the diameter of the inscribed circle of triangle OCF is 2, then find the product (AB).(CD)
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View Solution
