The mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
r=√59R
r=1√3R
r=R
r=√34R
To solve the problem, we need to find the point where the gravitational field is maximum given the mass density of a planet varies with distance from its center.
1. Understanding the Density Function:
The density of the planet is given as:
ρ(r)=ρ0(1−r2R2)
where ρ0 is a constant and R is the radius of the planet.
2. Finding the Mass Element:
The mass dm of a thin spherical shell of radius r and thickness dr can be expressed as:
dm=ρ(r)⋅dV=ρ(r)⋅4πr2dr
Substituting the expression for ρ(r):
dm=ρ0(1−r2R2)⋅4πr2dr
3. Calculating the Total Mass M(r):
To find the total mass M enclosed within radius r, integrate dm from 0 to r:
M(r)=∫r0dm=∫r0ρ0(1−r′2R2)4πr′2dr′
This can be simplified to:
M(r)=4πρ0∫r0(r′2−r′4R2)dr′
4. Performing the Integration:
Calculate the integral:
M(r)=4πρ0(r33−r55R2)
5. Gravitational Field E(r):
The gravitational field E at a distance r from the center is given by:
E(r)=GM(r)r2
Substituting M(r):
E(r)=G⋅4πρ0(r33−r55R2)r2=4πGρ03r−4πGρ05R2r3
6. Finding the Maximum Gravitational Field:
To find the maximum gravitational field, differentiate E(r) with respect to r and set it to zero:
dEdr=4πGρ03−12πGρ05R2r2=0
Rearranging gives:
4πGρ03=12πGρ05R2r2
Simplifying this leads to:
r2=5R29
Thus,
r=√59R
Conclusion:
The gravitational field is maximum at:
r=√53R
The density of the planet is given as:
ρ(r)=ρ0(1−r2R2)
where ρ0 is a constant and R is the radius of the planet.
The mass dm of a thin spherical shell of radius r and thickness dr can be expressed as:
dm=ρ(r)⋅dV=ρ(r)⋅4πr2dr
Substituting the expression for ρ(r):
dm=ρ0(1−r2R2)⋅4πr2dr
To find the total mass M enclosed within radius r, integrate dm from 0 to r:
M(r)=∫r0dm=∫r0ρ0(1−r′2R2)4πr′2dr′
This can be simplified to:
M(r)=4πρ0∫r0(r′2−r′4R2)dr′
Calculate the integral:
M(r)=4πρ0(r33−r55R2)
The gravitational field E at a distance r from the center is given by:
E(r)=GM(r)r2
Substituting M(r):
E(r)=G⋅4πρ0(r33−r55R2)r2=4πGρ03r−4πGρ05R2r3
To find the maximum gravitational field, differentiate E(r) with respect to r and set it to zero:
dEdr=4πGρ03−12πGρ05R2r2=0
Rearranging gives:
4πGρ03=12πGρ05R2r2
Simplifying this leads to:
r2=5R29
Thus,
r=√59R
The gravitational field is maximum at:
r=√53R
Similar Questions
A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionAn artificial satellite relolves around a planet for which gravitational force (F) varies with distance r from its centres as F∝r2 If v0 its orbital speed , then
View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :
View SolutionConsider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View SolutionThe mass density of a spherical galaxy varies as Kr over a large distance 'r' from its centre . In that region , a small star is in a circular orbit of radius R . Then the period of revolution , T depends on R as :
View SolutionConsider a spherical planet of radius R . Its density varies with the distance of its centre t as ρ=A−Br, where A and B are positive constants. Now answer the following questions.
Acceleration due to gravity at a distance r(r<R) from its centre is
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
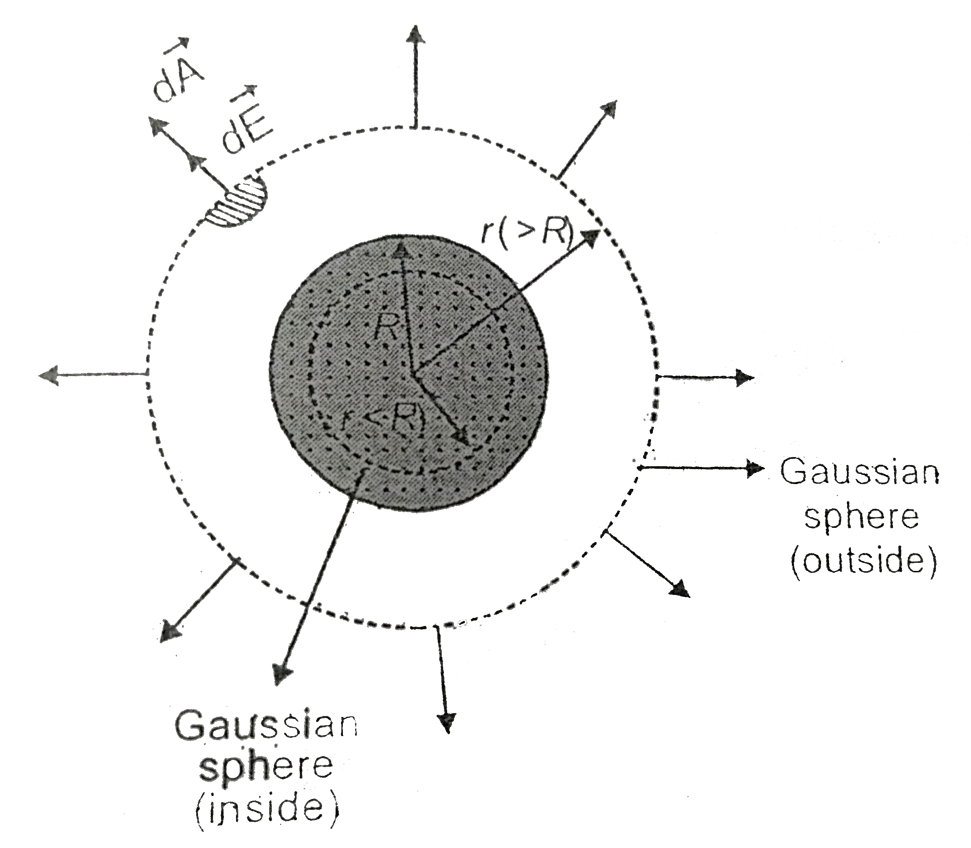
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]

View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View Solution
