Define the term work. Calculate the work done by a constant force. Is work done a scalar or a vector quantity ?
Step-by-Step Solution:
Step 1: Define Work
Work is defined as the product of the force applied to an object and the displacement of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅S⋅cos(θ)
where:
- W is the work done,
- F is the magnitude of the force,
- S is the magnitude of the displacement,
- θ is the angle between the force and the displacement vector.
Step 2: Calculate Work Done by a Constant Force
When a constant force is applied, the work done can be calculated using the same formula. If the force is constant and the displacement is known, the work done can be simplified to:
W=F⋅S⋅cos(θ)
For example, if a constant force of F=10N is applied to move an object a distance of S=5m in the direction of the force (θ=0∘), then:
W=10N⋅5m⋅cos(0∘)
Since cos(0∘)=1:
W=10N⋅5m⋅1=50J
Step 3: Determine if Work is a Scalar or Vector Quantity
Work is a scalar quantity. This can be understood from the mathematical expression of work, which involves the dot product of the force and displacement vectors:
W=F⋅S
The result of a dot product is always a scalar, indicating that work does not have a direction associated with it, unlike vector quantities.
Work is defined as the product of the force applied to an object and the displacement of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅S⋅cos(θ)
where:
- W is the work done,
- F is the magnitude of the force,
- S is the magnitude of the displacement,
- θ is the angle between the force and the displacement vector.
When a constant force is applied, the work done can be calculated using the same formula. If the force is constant and the displacement is known, the work done can be simplified to:
W=F⋅S⋅cos(θ)
For example, if a constant force of F=10N is applied to move an object a distance of S=5m in the direction of the force (θ=0∘), then:
W=10N⋅5m⋅cos(0∘)
Since cos(0∘)=1:
W=10N⋅5m⋅1=50J
Work is a scalar quantity. This can be understood from the mathematical expression of work, which involves the dot product of the force and displacement vectors:
W=F⋅S
The result of a dot product is always a scalar, indicating that work does not have a direction associated with it, unlike vector quantities.
Similar Questions
Knowledge Check
Work done by frictional force
AIs always negativeBIs always positiveCIs zeroDMay be positive, negative or zeroWork done by a frictional force is
AnegativeBpositiveCzeroDall of the aboveCalculate the work done for B → A, :-
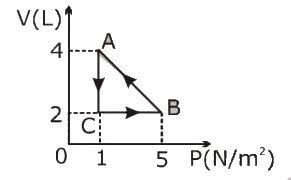 A6×10−3jB12×10−3jC3×10−3jD4×10−3j
A6×10−3jB12×10−3jC3×10−3jD4×10−3j
