Proceeding from geometric reasoning, prove that :
(a) if the function f(x) increases and has a concave graph in the interval [a,b], then
(b,a)f(a)<∫baf(x)dx<(b−a)f(a)+f(b)2
(b) if the function f(x) increases and has a convex graph in the interval [a,b], then
(b−a)f(a)+f(b)2<∫baf(x)dx<(b−a)f(b)
The correct Answer is:The inequality
(b−a)f(a)<∫baf(x)dx is obvious.
Topper's Solved these Questions
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6 . 4 (Changing the Variable in a Definite Integral)
30 Videos
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6. 5 (Simplification of Integrals Based on the Properties of Symmetry of Integrands)
14 Videos
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6.2 (Evaluating Definite Integrals by the Newton-Leibnitz formula)
17 Videos
- INTRODUCTION OF MATHEMATICAL ANALYSISBOOK - IA MARONCHAPTER - INTRODUCTION OF MATHEMATICAL ANALYSISEXERCISE - Additional Problems
34 Videos
Similar Questions
Compute in integral ∫√2−√3√4−x2dx
View SolutionWhat is the value the integral ∫1−1|x|dx ?
View SolutionEvaluate: ∫√31dx1+x2
View SolutionProve the inequalities :
(a) n!<(n+12)n for a natural n>1:
(b) 13.34.56......2n−12n<1√2n+1
View SolutionIf f is a continuous function on the interval [a,b] and there exists some c in(a,b) then prove that int_(a)^(b)f(x)dx=f(c)(b-a)
View SolutionIf |int_(a)^(b)f(x)dx|=int_(a)^(b)|f(x)|dx,a
View Solutionमान लीजिए [a ,b ] पर परिभाषित एक फलन f है इस प्रकार की सभी x∈(a,b)के लिए f'(x)<0है तो सिद्ध कीजिए की (a ,b ) पर f एक वर्धमान फलन है।
View Solutionयदि फलन f'(x) और g(x) बंद अंतराल [ab] में संतत हो तथा खुले अंतराल (a,b) में अवकलनीय हो तो दिखाए की काम-से-कम एक ऐसा c मिलेगा जहां a<c<b ताकि
∣∣∣f(a)f(b)g(a)g(b)∣∣∣=(b−a)∣∣∣f(a)f'(c)g(a)g'(c)∣∣∣
View Solution∫badx=∫caf(x)dx+∫caf(x)dx,a<c<b.
View SolutionIf a<b<c∈R and f(a+b+c−x)=f(x) for all, x then ∫bax(f(x)+f(x+c))dxa+b is:
View SolutionLet f (x) be a polynomial function of degree 3 where a<b<candf(a)=f(b)=f(c). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c>|a|)
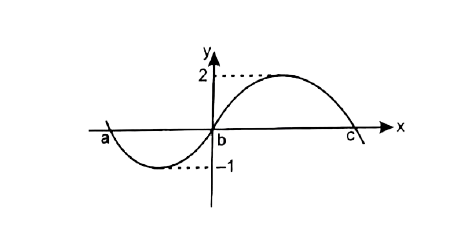
View SolutionIf a<b<c∈R and f(a+b+c−x)=f(x) for all, x then ∫bax(f(x)+f(x+c))dxa+b is:
View Solutionयदि f अंतराल [ a,b] में सतत फलन है तथा एक c∈(a,b) अस्तित्व में है, तो सिद्ध कीजिये कि ∫baf(x)dx=f(c)(b−a) हैं।
View SolutionLet f (x) be a polynomial function of degree 3 where a<b<candf(a)=f(b)=f(c). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c>|a|)
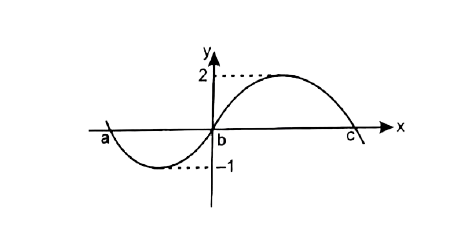
View SolutionIf a<b<c∈R and f(a+b+c−x)=f(x) for all, x then ∫bax(f(x)+f(x+c))dxa+b is:
View Solution

