Find the are length of the cardioid ρ=a(1+cosφ)(a>0,0≤φ≤2π)
The correct Answer is:8a
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Area of Surface of Revolution
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Geometrical Applications of the Definite Integral
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Curve Represented Parametrically
4 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Find the area of the surface formed by revolving the astroid x2/3+y2/3=a2/3 about the x-axis
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
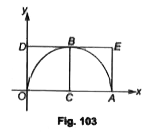
View SolutionCompute the are length of the involute of a circle x=a(cost+tsint),y=a(sint−tcost) from t=0 to t=2π.
View SolutionProve that for the function y=αx2+βx+γ the number ξ in the Lagrange formula ,used on an arbitrary interval [a,b] is the arithmetic mean of the numbers a and b : ξ=(a+b)/2
View SolutionIntegration of other transcendental functions
I=∫Inxdx√1−x.
View SolutionIf φ(x) is differentiable function ∀x∈R and a∈R+ such that φ(0)=φ(2a),φ(a)=φ(3a)andφ(0)≠φ(a) then show that there is at least one root of equation φ′(x+a)=φ′(x)∈(0,2a)
View SolutionIf cosx−sinx≥1and0≤x≤2π , then find the solution set for x .
View SolutionIf 0≤x≤2πand|cosx|≤sinx, the
View Solutionक्या φ(x),x=1 पर संतत है जबकि
φ(x)={x+3,0≤x≤14−x,x>1?
View SolutionCompute the area of the figure bounded by the circle ρ=3√2acosφandρ=3asinφ
View SolutionFind the area of the figure out only by the circle ρ=√3sinφ from the cardioid ρ=1+cosφ
View SolutionCompute the volume of the solid obtained by revolving about the polar axis the cardioid ρ=a(1+cosφ) shown in
View SolutionFind the length of the logarithmic spiral ρ=aemϕ between a certain point (ρ0,φ0) and a moving point (ρ,φ)
View SolutionFind the length of the lemniscate ρ2=2a2cos2φ between the right-hand vertex corresponding to φ=0 and any point with a polar angle φ<π4
View SolutionCompute the length of the segment of the straight line ρ=asec(φ−π3) between φ=0andφ=π2
View Solution

