An infinitely long line charge having a uniform charge per unit length λ lies a distance d. From center of imaginary sphere of radius R. Then
Flux crossing the sphere is zero if d gt R b)
Flux crossing the sphere is 2λ√R2−d2ε0 , if d<R
If d>R, the magnitude of maximum potential difference two points on the sphere is λ2πε0In(d+Rd−R)
When a charge is moved along any dimeter of the sphere in the plane perpendicular to the wire, work done is zero.
The correct Answer is:A, B, C
Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
Explore 2 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED)MATRIX MATCHING TYPE QUESTIONS)
Explore 1 Video
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 20 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 6 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 9 Videos
Similar Questions
An empty thick conducting shell of inner radius a and outer radius b is shown in figure. If it is obseved that the inner face of the carries a uniform charge density −σ and the surface carries a uniform charge density .σ.

If a point charge qA is placed at the center of the shell, then choose the correct statement(s)
View SolutionIn fig. each +q. arefixed at L and M.O is the point of distance LM.X and Y axes are as shown. Consider the situations given in Column - I and match with the information in Column - II

View SolutionFigure shows an electric line of force which curves along a circular are. The magnitude of electric field intensity is same at all points on this curve and is equal to E. If potential at A is V them the potential at B is :

View SolutionWhat is the radius of the path of an electron (mass 9 × 10-31 kg and charge 1.6×x10–19 C) moving at a speed of 3×x107 m/s in a magnetic field of 6x×10−4 T perpendicular to it? What is its frequency? Calculate its energy in keV. (1eV=1.6×10−19J)
View SolutionFind the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
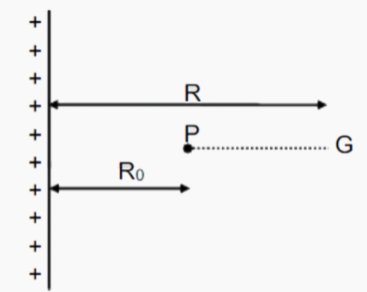
View SolutionAn infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where Rltd and Rgtd.

View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionA half ring of radius R has a charge of lambda per unit length. The electric force on 1C charged placed at the center is
View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View Solutionअनन्त रेखीय आवेश जिसके इकाई लम्बाई पर आवेश की मात्रा λ हो तो इससे r दूरी पर विघुत क्षेत्र की तीव्रता का मान होगा-
View Solutionअनन्त रेखीय आवेश जिसके इकाई लम्बाई पर आवेश की मात्रा λ हो तो इससे r दूरी पर विघुत क्षेत्र की तीव्रता का मान होगा-
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png)
View SolutionA uniformly charged and infinitely long line having a linear charge density lambda . is placed at a normal distance y from a point O. Consider a sphere of radius R with with O as centre and R gt y . Electric flux through the surface of the sphere is
View Solution

