Some of notable matters in derivation of M→A=→Fext. Solution in Gujrati
(1) To determine the motion of the centre of mass no knowledge of internal forces of the system of particles is required for this purpose to know only the external forces.
(2) To obtain this equation we did not need to specify the nature of the system of particles. The system may be a collection of particles in which there may be all kinds of internal motion, or it may be a rigid body which has either pure translational motion or a combination of translational and rotational motion.
(3) Whatever is the system and the motion of its individual particles, the centre of mass moves according to M→A=→Fext.
Similar Questions
Explain the physical significance of the equation M→A=→Fext, where 'M' is the mass of the whole rotating body and →A is the acceleration of the centre of mass of the system of particles.
View SolutionEquation MvecA=vecF_(ext) denote what?
View SolutionDerive the equation W=−PextΔV
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
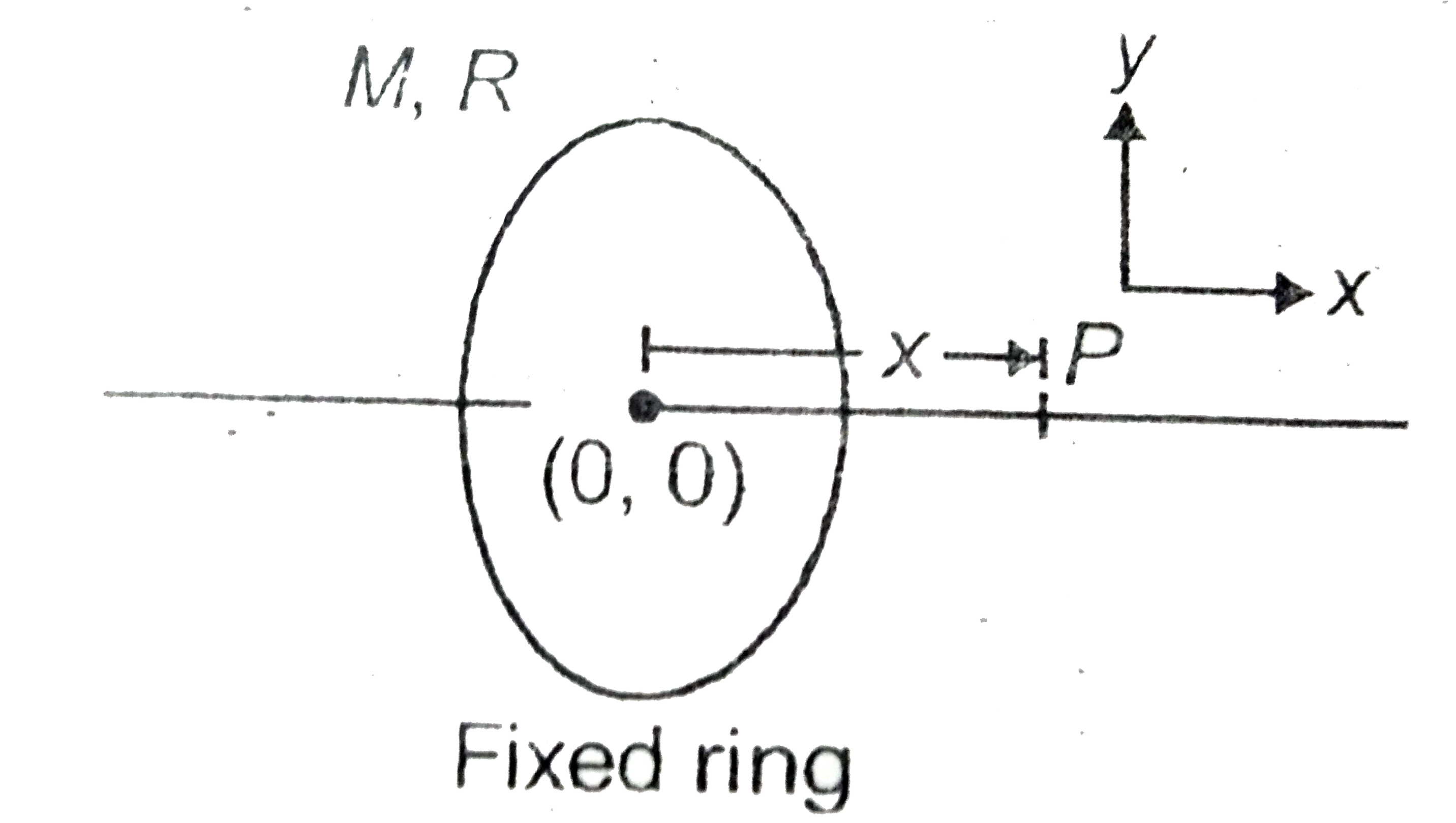
The value of maximum gravitational field intensity is
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
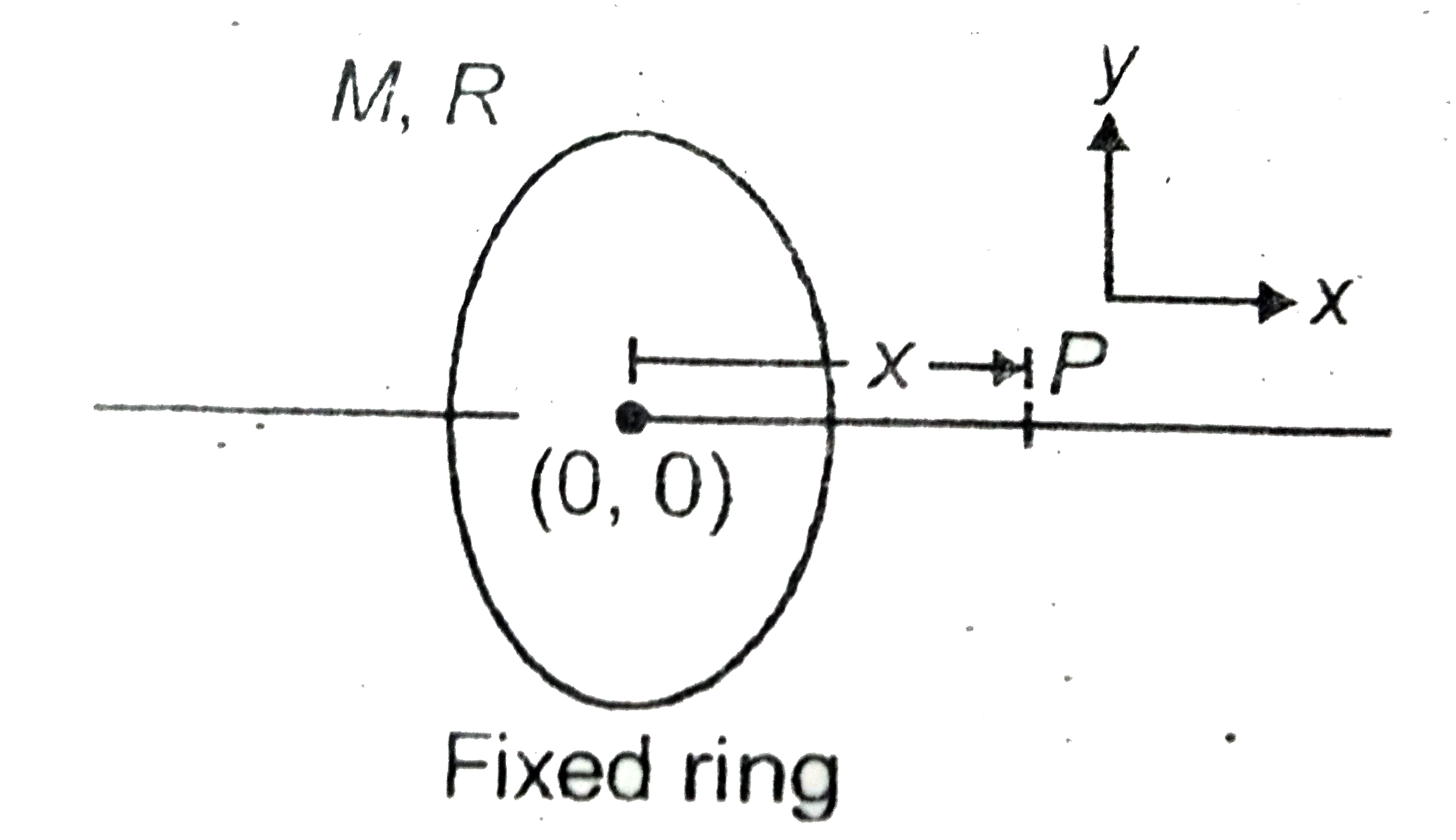
The gravitational field is zero at x equal to
View SolutionThe gravitational force vec(F) upon an object of mass m placed in external gravitational field vec(E )_("ext") is given by vec(F)=m vec(E )_("ext") . Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction. For a point near to the centre i.e., x lt lt R, the intensity of gravitational field E
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
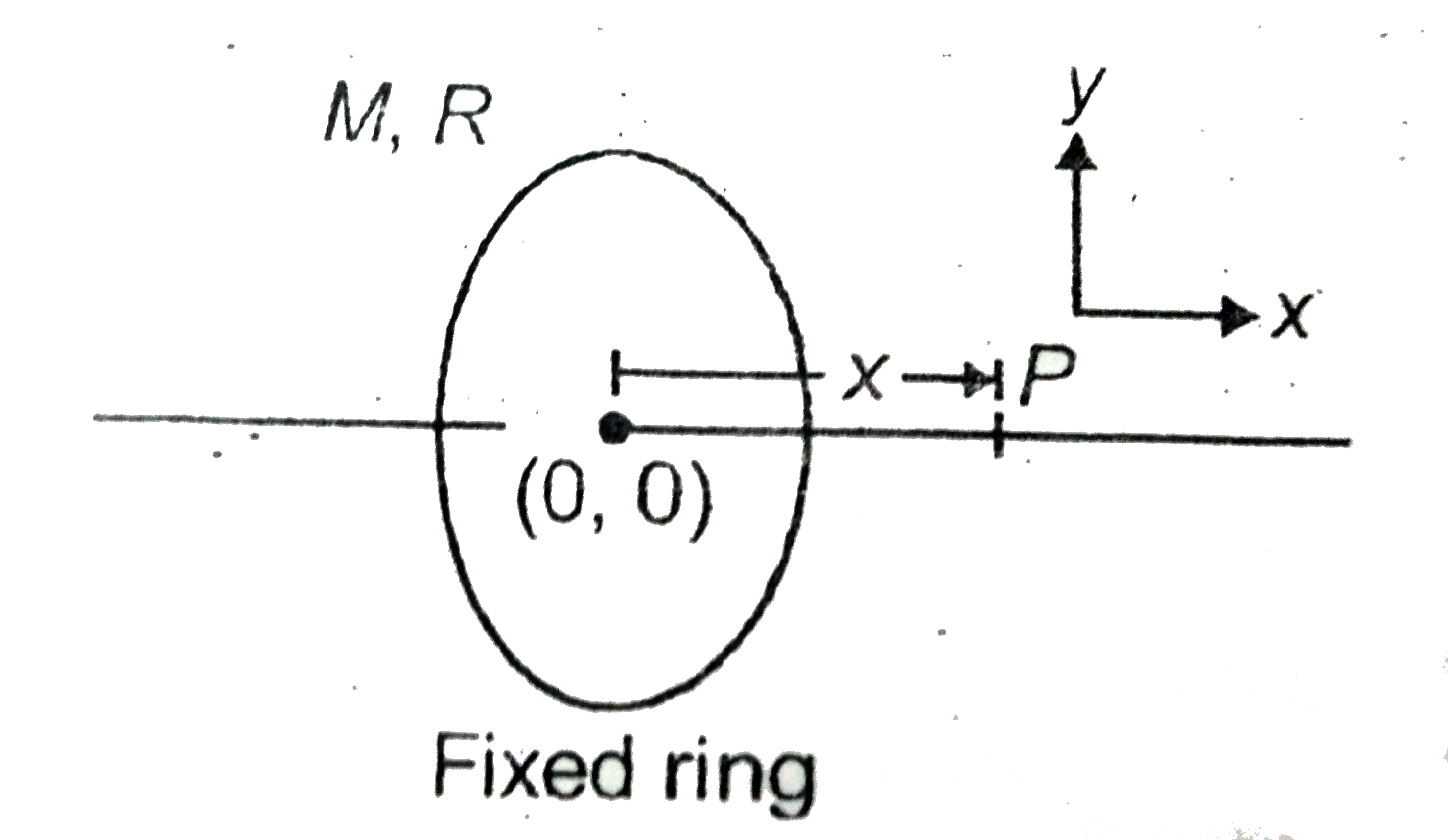
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speed
View Solution

