Fifty seeds were selected at random from each of 5 bags of seeds , and were kept under standardised conditions favourable to germination. After 20 days. the number of seeds which had germinated in each collection were counted and recorded as follows :
Bag12345Number of seeds4048423941germinated
What is the probability of germination of
more than 40 seeds in a bag ?
The correct Answer is:0.6
To solve the problem of finding the probability of germination of more than 40 seeds in a bag, we can follow these steps:
1. Identify the Data: We have the number of seeds that germinated from each of the 5 bags:
- Bag 1: 40 seeds
- Bag 2: 48 seeds
- Bag 3: 42 seeds
- Bag 4: 39 seeds
- Bag 5: 41 seeds
2. Determine the Favorable Cases: We need to count how many bags had more than 40 seeds germinated.
- Bag 1: 40 (not more than 40)
- Bag 2: 48 (more than 40)
- Bag 3: 42 (more than 40)
- Bag 4: 39 (not more than 40)
- Bag 5: 41 (more than 40)
From the above, we see that bags 2, 3, and 5 have more than 40 seeds germinated. Thus, there are 3 favorable cases.
3. Total Number of Bags: The total number of bags is 5.
4. Calculate the Probability: The probability (P) of germination of more than 40 seeds in a bag is given by the formula:
P(more than 40 seeds)=Number of favorable casesTotal number of cases=35
5. Convert to Decimal: To express this probability in decimal form:
P=35=0.6
Final Answer:
The probability of germination of more than 40 seeds in a bag is 0.6.
---
- Bag 1: 40 seeds
- Bag 2: 48 seeds
- Bag 3: 42 seeds
- Bag 4: 39 seeds
- Bag 5: 41 seeds
- Bag 1: 40 (not more than 40)
- Bag 2: 48 (more than 40)
- Bag 3: 42 (more than 40)
- Bag 4: 39 (not more than 40)
- Bag 5: 41 (more than 40)
P(more than 40 seeds)=Number of favorable casesTotal number of cases=35
P=35=0.6
The probability of germination of more than 40 seeds in a bag is 0.6.
Topper's Solved these Questions
- PROBABILITY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY Exercise:Skill Testing Exercise
Explore 8 Videos
- PROBABILITY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY Exercise:EXERCISE 15.1
Explore 23 Videos
- LINE AND ANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LINE AND ANGLESExercise:Multiple Choice Questions MCQs)
Explore 10 Videos
- SURFACE AREAS AND VOLUMESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SURFACE AREAS AND VOLUMESExercise:MULTIPLE CHOICE QUESTIONS
Explore 18 Videos
Similar Questions
An unbiased coin is tossed 20 times. In this experiment , 11 heads and 9 tails were received. Calculate the probability of receiving head and the probability of receiving tail on the basis of the experiment .
View SolutionIn a cricket match, Dhoni hits a boundary 6 times out of 30 balls he plays. Find the probability that he did not hit a boundary.
View SolutionThe measure of the complementary angle of an angle with measure 40∘ is .............
View SolutionThe total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm2.
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardized conditions favorable to germination. After 20 days, the number of seeds which had germinated in each collection were counted and recorded as follows
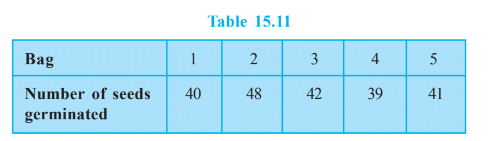
What is the probability of germination of
(i) more than 40 seeds in a bag?
(ii) 49 seeds in a bag?
(iii) more that 35 seeds in a bag?
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardised conditions favourable to germination. After 20 days the number of seeds which had germinated in each collection were counted and recorded as follows:
Bag12345No. of seeds germinated:4048423941 What is the probability of germination of:
(i)more than 40 seeds in a bag? (ii)49 seeds in a bag? (iii)more than 35 seeds in a bag (iv)at least 40 seeds in a bag? (v)at most 40 seeds in a bag?
View SolutionFifty seeds were selected at random from each 5 bags of seeds and were kept under standardised conditions favourable to germination .
After 20 days , the number of seeds which had germinated in each collection were counted and recorded as follows :

What is the probability of germination of
(i) more than 40 seeds from a bag ?
(ii) 49 seeds from a bag ?
(iii) more than 35 seeds from a bag ?
View Solutionबीजों के 5 थैलों में से प्रत्येक थैले से पचास बीज यदृच्छया चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं । 20 दिन बाद प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिन कर नीचे दर्शाए अनुसार एक सारणी में लिखी गई ।

निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या है ? (
(i) एक थैले में40 से अधिक बीज ?
(ii ) एक थैले में 49 बीज
(iii ) एक थैले में 35 से अधिक बीज ।
View Solutionबीजो के 5 थैलो में से प्रत्येक थैले से पचास बीच यदृच्छया चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल है। 20 दिनों बाद प्रत्येक संग्रह में अंकुरित हुए बीजो की संख्या गईं कर नीचे दर्शाए अनुसार एक सारणी में लिखी गई।
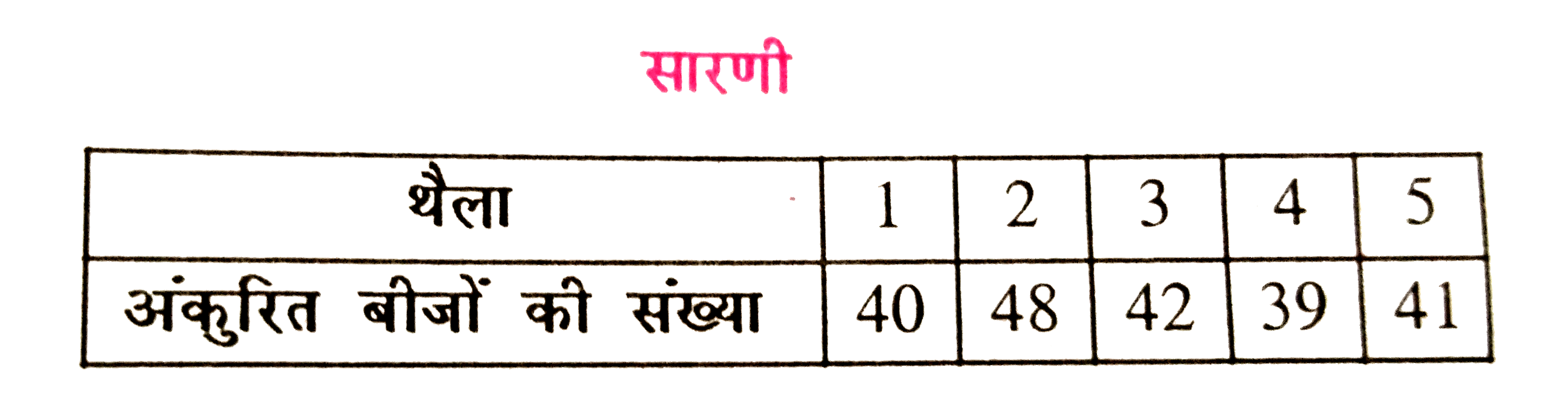
निम्नलिखित बीजो के अंकुरण की प्रायिकता क्या है?
(i) एक थैले में 40 से अधिक बीज?
(ii)एक थैले में 49 बीज
(iii) एक थैले में 35 से अधिक बीज
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardised condition favourable to germination. After 20 days, the number of seeds which had germinated in each collection were conducted and as follows

What is the probablity of germination of
(i) More than 40 seeds in a bag.
(ii) 49 seeds in a bag
(iii) More than 35 seeds in a bag
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardised conditions favourable to germination. After 20 days, the number of seeds which had germinated in each collection were counted and recorded as follow
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardised conditions favourable to germination. After 20 days, the number of seeds which had germinated in each collection were counted and recorded as follows: (Bag - Number of seeds germinated) 1-40 2-48 3-40 4-35 5-45 what is the probability of germination of more than 40 seeds in a bag?
View SolutionFifty seeds were selected at random from each of 5 bags of seeds, and were kept under standardised conditions favourable to germination. After 20 days the number of seeds which had germinated in each collection were counted and recorded as follows:
Bag12345No. of seeds germinated:4048423941 What is the probability of germination of:
(i)more than 40 seeds in a bag? (ii)49 seeds in a bag? (iii)more than 35 seeds in a bag (iv)at least 40 seeds in a bag? (v)at most 40 seeds in a bag?
View SolutionFifty seeds were selected at random from each of 5 bags of seeds , and were kept under standardised conditions favourable to germination. After 20 days. the number of seeds which had germinated in each collection were counted and recorded as follows :
Bag12345Number of seeds4048423941germinated
What is the probability of germination of
49 seeds in a bag ?
View SolutionFifty seeds were selected at random from each of 5 bags of seeds , and were kept under standardised conditions favourable to germination. After 20 days. the number of seeds which had germinated in each collection were counted and recorded as follows :
Bag12345Number of seeds4048423941germinated
What is the probability of germination of
more that 35 seeds in a bag ?
View Solution