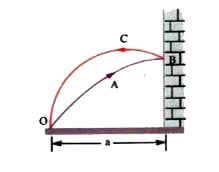
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance .a. from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
As we have discussed in the theory, the horizontal component of the velocity of ball during the path OAB is ucosα while in its return journey BCO it is eucoaα. fThe time of fight T also remains unchanged. Hence,
T=tOAB+tBCOor2usinαg=aucosα+aeucosα
(or) aeucosα=2usinαgaucosα
(or )aeucosα=2u2sinαcosα−aggucosα
∴e=ag2u2sinαcosα−agore=1(u2sin2αag−1)
Topper's Solved these Questions
- COLLISIONS Book:AAKASH SERIESChapter:COLLISIONS Exercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 12 Videos
- COLLISIONS Book:AAKASH SERIESChapter:COLLISIONS Exercise:NUMERICAL EXERCISE ( LEVEL 1)
Explore 18 Videos
- CENTRE OF MASSBook:AAKASH SERIESChapter:CENTRE OF MASSExercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
Explore 3 Videos
- ELASTICITYBook:AAKASH SERIESChapter:ELASTICITYExercise:Questions for Descriptive Answers
Explore 10 Videos
Similar Questions
What is a collision ? Mention the types of collisions
View SolutionA 2 kg mass moving with a velocity of 10mS−1 collides with another 6 kg mass moving in opposite direction with a velocity of 20ms−1 During collision, they stick together. Find the magnitudes of their common velocity and the momentum.
View SolutionA man (m1) with a bag (m2) in hand falls freely vertically from a height h above the ground. After falling through a height y0, man throws bag horizontally with a velocity u0 towards his right.
View SolutionA steel wire of area of cross-section A and length 2L is clamped firmly between two points seperated by a distance .2L.. A body is hung from the middle point of the wire such that the middle point sags by a distance X. Calculate the mass of the body and the angle made by the string with the horizontal. (Young.s modulus of Steel = y)
View SolutionA ball is projected from the ground with speed u at an angle alpha with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
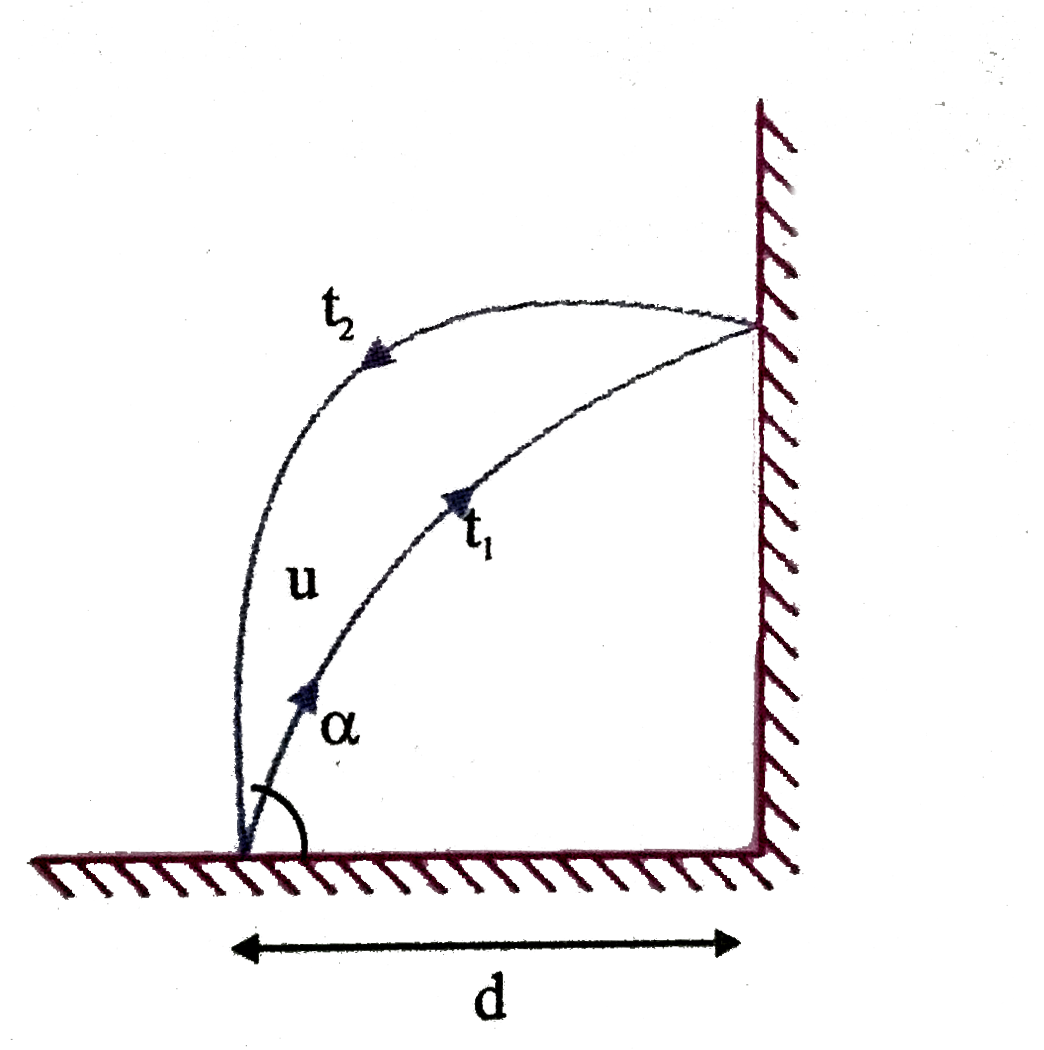
The total time of journey of the ball is
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
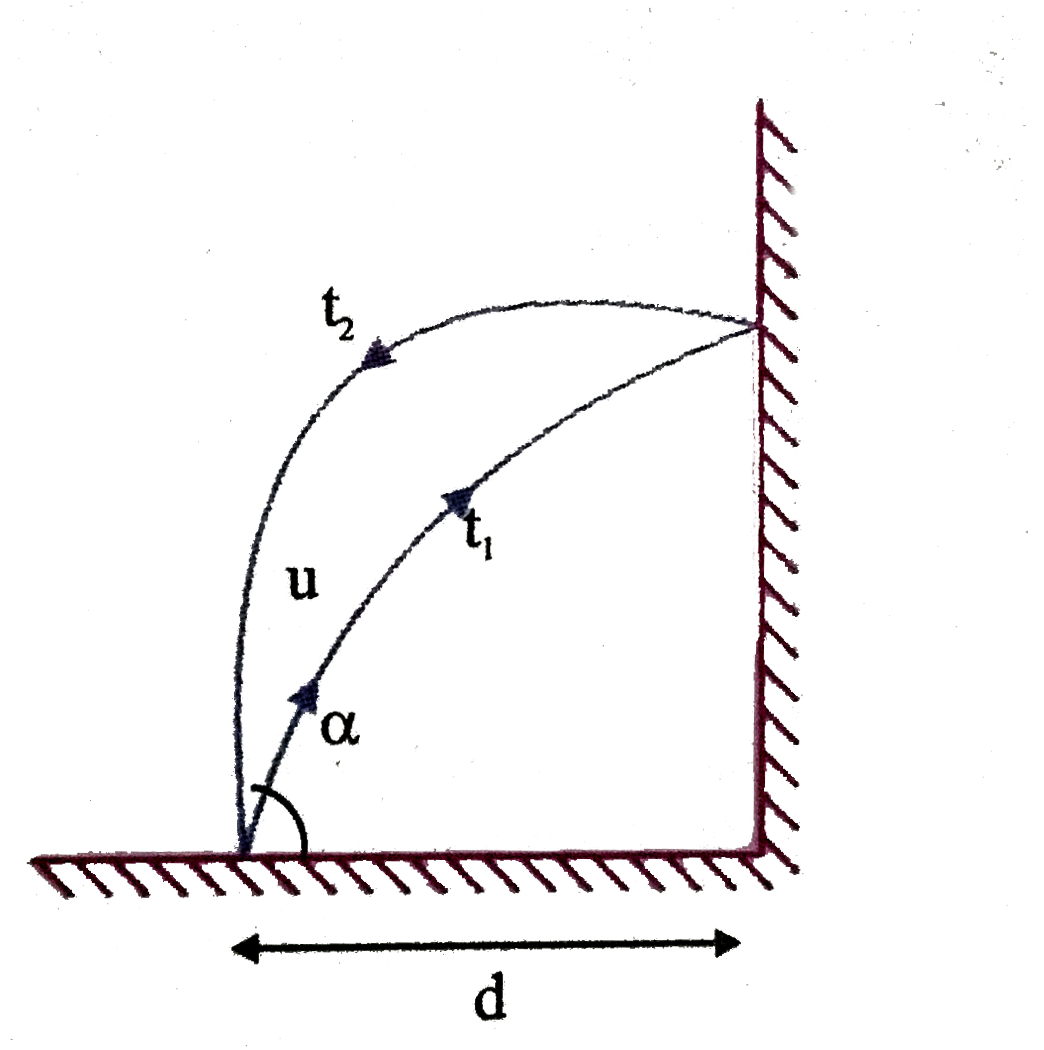
The horizontal distance 'd' from the wall is
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'alpha' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e' ) If the line joining the point of projection and the point of impact makes an angle 'theta' with the horizontal, then tan theta is
View SolutionTwo identical smooth balls are projected towards each other from points A and B on the horizontal ground with same speed of projection. The angle of projection in each case is 30^(@) . The distance between A and B is 100m . The balls collide in air and return to their respective points of projection. If coefficient of restitution is e = 0.7 , find (a) the speed of projection of either ball. (b) coordinates of point with respect to a point of projection of A , where the balls collide. (Take g = 10 m//s^(2) )
View SolutionA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :

View SolutionFrom a point on smooth floor of a room a toy ball is shot to hit a wall. The ball then returns back to the point of projection. If the time taken by ball in returining is twice the time taken in reaching the wall find the coefficient of restitution:
View SolutionA ball projected from ground at an angle of 45∘ just clears a wall infront. If point of projection is 4m from the foot of wall and ball strikes the ground at a distance of 6m on the other side of the wall, the height of the wall is
View SolutionA ball projected from the ground with speed 10m/s at an angle of 45^(@) with horizontal. It collides with a wall at a distance 2 m from the point of projection and returns to its original position. If the coefficient of restitution between the ball and wall is 1/x, find x.
View SolutionA ball is projected from ground with a speed 70m//s at an angle 45^(@) with the vertical so that it strikes a vertical wall at horizontal distance (490)/(3)m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA ball is projected from the ground with speed u at an angle alpha with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
View Solution

