Two wires made of materials of Young.s moduli 160 and 200 GPa have lengths in the ratio 3 : 4 and radii 2:3. For the same elongation, what must be the ratio of the loads on them
The correct Answer is:64:135
Topper's Solved these Questions
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Numerical (Exercise) (LEVEL - 2)
22 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Very Short Answer Type Questions
15 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
Similar Questions
A wire 4 m long and cross section 3×10−6m2is stretched by Imm. If its Young.s modulus is 2×1011N/m2, find the energy stored in the wire.
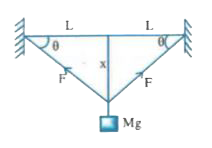
View SolutionA steel wire of area of cross-section A and length 2L is clamped firmly between two points seperated by a distance .2L.. A body is hung from the middle point of the wire such that the middle point sags by a distance X. Calculate the mass of the body and the angle made by the string with the horizontal. (Young.s modulus of Steel = y)
View SolutionThe increase of length of a wire under a load is equal to its initial length. What is the stress in the wire equal to?
View SolutionFour identical balls A,B,C and D are placed in a line on a frictionless horizontal surface. A and D are moved with same speed .u. towards the middle as shown. Assuming elastic collisions, find the final velocities.
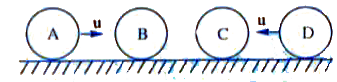
View SolutionFind the components of vector →A=2ˆi+3ˆj along the directions of ˆi+ˆj and ˆi−ˆj.
View SolutionTwo wires of the same material and length are stretched by the same force. Their masses are in the ratio 3:2 . Their elongations are in the ratio
View SolutionTwo pieces of wire, A and B of the same material have their lengths in the ratio 1:3 and their diameters are in the ratio 2:1 . If they are stretched by the same force, their elongations will be in the ratio
View SolutionTwo wires of same material and length are stretched by the same force. If the ratio of radii of the two wires in n:1 then the ratio of their elongation is
View SolutionTwo wires have the same material and length, but their masses are in the ratio of 4:3. If they are stretched by the same force, their elongations will be in the ratio of
View SolutionTwo wire of the same material and length stretched by the same force. If the ratio of the radii of the two wires is n : 1 then the ratio of their elongations is
View SolutionTwo wires of same material have masses in the ratio 3:4 the ratio of their extensions under the same load if their lengths are in the ratio 9:10 is
View SolutionTwo wires of same material have masses in the ratio 3:4 the ratio of their extensions under the same load if their lengths are in the ratio 9:10 is
View SolutionThere are two wires of same material. Their radii and lengths are both in the ratio 1:2. If the extensions produced are equal, what is the ratio of the loads?
View SolutionThere are two wires of same material. Their radii and lengths are both in the ratio 1:2. If the extensions produced are equal, what is the ratio of the loads?
View SolutionTwo wires have masses in the ratio 3:4. They are made of the same material. Under the same load what is ratio of their elongations ? Explain why?
View Solution

