A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l/4. The pendulum is released from rest. Throughout the motion the moving string makes small angle wilth vertical. Find the time after whcih the pendulum returns back to its initial position.
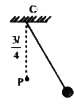
After P length of pendulum becomes 14
Now as T∝√l so after P time period will become
T1=T/2. Therefore, the disered time will be
t=T2+T2=T2+T4=3T4
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A praticle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle is subjected to two S H Ms x1=A1sinwt and x2=A2sin(wt+π/4). The resultant S H M will have an amplitude of
View SolutionThe displacement of two particles executing S.H.M are represented by y1=asin(wt+ϕ) and y2=acoswt. The phase difference between the velocities of these particles is
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find the amplitude and the time period of the motion of the block.

View SolutionWhat is Physics ?
View SolutionA pendulum has a period T for small osillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.
View SolutionA small bob attached to a light inextensible thread of length l has a periodic time T when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end O of a vertical rigid rod of length 3l//4 . If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be
View SolutionA nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60^(@) with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionA small bob attached to a light inextensible thread of length l has a periodic time T when
allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end O of a vertical rigid rod of length 3l4 (as in figure). If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be-
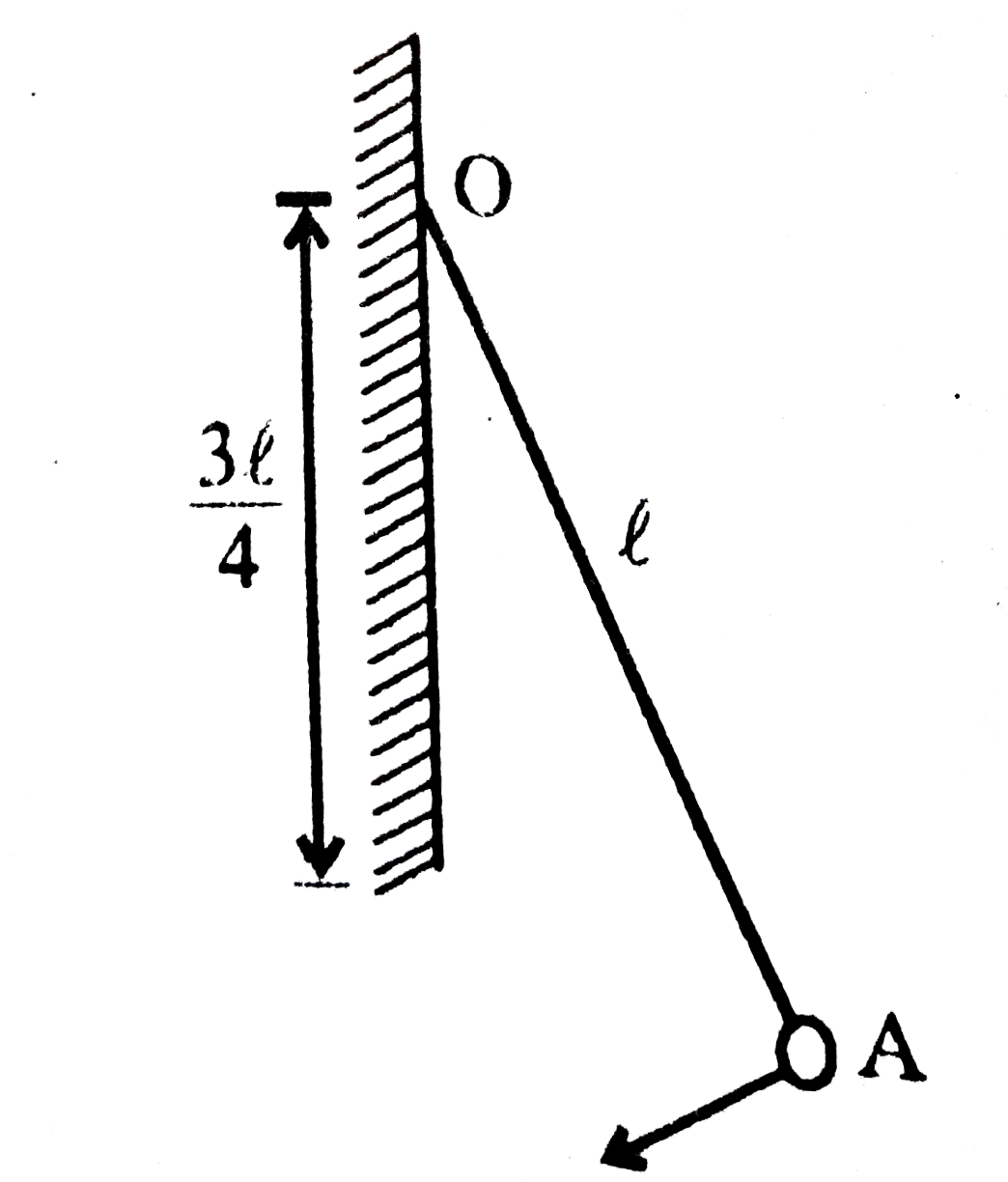
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
View SolutionA particle pendulum is positioned such that is centre of gravity is vertically above suspension point. From that position the pendulum started moving tward the stable equilibroum and passed it with an angular velocity ω. By neglecting the friction at point of suspension, the period of small oscillations of the pendulum is
View SolutionA nail is fixed at a point P vertically below the point of suspension 'O' of simple pendulum of length 1m. The bob is released when the string of pendulum makes an angle 30∘ with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with P . The least distance of P from O is
View SolutionA simple pendulum oscillating with a small amplitude has a time period of T = 1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulum
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of sigma C//m^2 . [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle beta with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View SolutionA simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
View SolutionA pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance (3l)/4 . The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
View Solution

