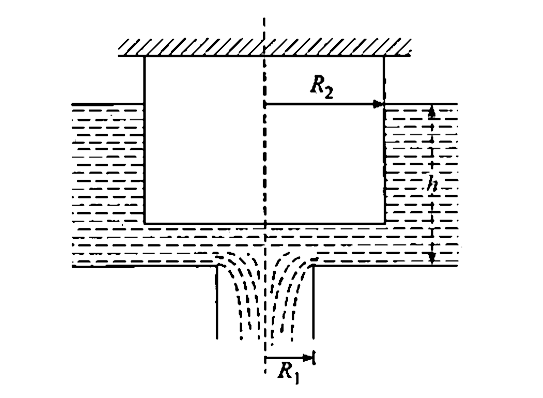
The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R(2)>R1 The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. Find the static pressure of the fluid in the clearance as a function of the distance from the axis of the orifice and the cylinder), if the height of the fluid is

Pa+ρgh[1−R21r2]
Topper's Solved these Questions
- FLUID MECHANICSBook:AAKASH SERIESChapter:FLUID MECHANICSExercise:Numerical Exercise (LEVEL-2)
Explore 18 Videos
- EXPANSION OF SOLIDS Book:AAKASH SERIESChapter:EXPANSION OF SOLIDS Exercise:Questions for Descriptive Answers
Explore 5 Videos
- FRICTION Book:AAKASH SERIESChapter:FRICTION Exercise:ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
Explore 1 Video
Similar Questions
An open rectangular ank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side (a) Determine the maximum acceleration that can be given without spilling the water.
(b) Calculate the percentage of water split over, if this accelerationis increased by 20%
(c ) If initially the tank is closed at the top and is accelerated horizontally by 9m/s2, find the gauge pressure at the bottom of the front and rear walls of the tank.

View SolutionThe length of an iron rod is measured by a brass scale. When both of them are at 20∘C, the length is 80 cm. What is the length of the rod at 100∘C as measured by the scale at 100∘C? The coefficient of linear expansion of brass and iron are 24×10−6(C∘)−1and18×10−6(C∘)−1 respectively.
View Solutionif the man can move with maximum acceleration a1anda2 relative to the trolley car in forward and backward directions, respectively then :
View SolutionThe horizontal bottom of wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1 (figure). The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. Find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder), if the height of the fluid is equal to h.

View SolutionThe horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1figure. The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder) , if the height of the fluid is equal to h.
View SolutionIf a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
View Solutionएक बर्तन की तली क्षेत्रफल A तथा इसमें भरे द्रव का घनत्व d एवं ऊंचाई h है द्रव का दाब कितना होगा
(i) बर्तन की तली पर
(ii) द्रव के ऊपरी पृष्ठ पर
View Solutionद्रव से भरे पात्र की तली पर दाब निर्भर नहीं करता है-
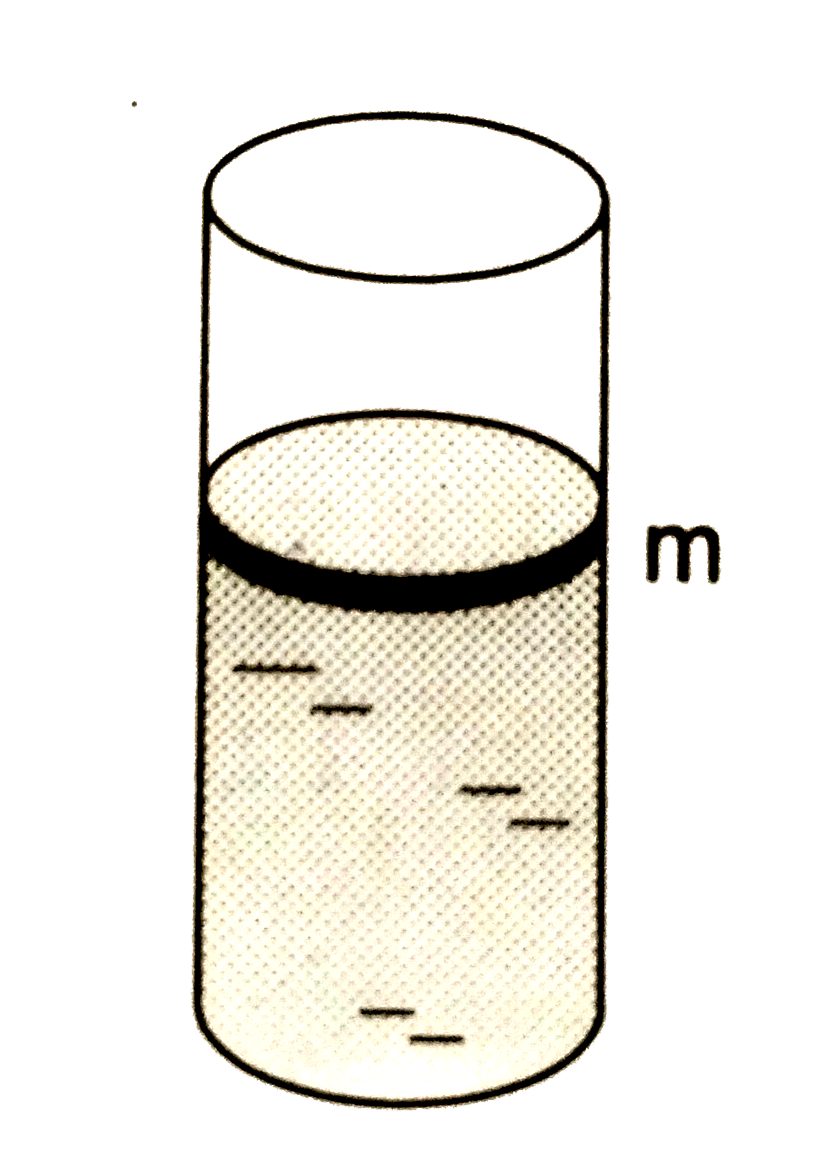
View Solutionत्रिज्या R वाले एक बेलनाकार बरतन में एक द्रव रखा गया है | इस द्रव के ऊपर बरतन में m द्रव्यमान का एक पिस्टन फिट है जो बरतन कि दीवारों से वायुरुद्ध प्रकार से सटा है, पर वहाँ किसी प्रकार का घर्षण नहीं है | यदि बरतन में द्रव कि ऊंचाई h तथा उसका घनत्व ρ हो तो बरतन कि पेंदी पर द्रव का दाब निकालें |
View Solutionद्रव को एक बेलनाकार पात्र में रखकर पात्र को उसकी अक्ष के सापेक्ष घुमाने पर द्रव पात्र की दीवारों के पास उठता है । यदि पात्र की त्रिज्या 0.05 मीटर और घूर्णन दर 2 चक्कर /सेकंड हो तो पात्र के किनारे व केंद्र के मध्य ऊँचाई में अंतर मीटर में होगी -
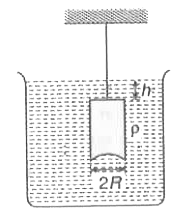
View SolutionR त्रिज्या के एक बेलन की तली से R त्रिज्या का ही अर्द्धगोलाकार भाग अलग कर दिया जाता है। शेष बचे बेलनाकार भाग का आयतन V तथा द्रव्यमान M है। इस भाग को एक डोरी द्वारा ऊर्ध्वाधर ρ' घनत्व वाले द्रव में लटका दिया जाता है। बेलन का ऊपरी सिरा द्रव के पृष्ठ से h गहराई पर है। द्रव द्वारा बेलन के निचले सिरे पर आरोपित बल है
View SolutionA tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
View SolutionFluid is placed in a cylindrical vessel. The vessel is rotated perpendicular to the vertical axis passing through the center of the base, radius r and angular velocity of the vessel omega Then find the difference in height of the fluid at the center and sides of the vessel.
View SolutionIf a vessel containing a fluid of density rho upto height h is accelerated vertically downwards with acceleration a_(@) then the pressure by fluid at the bottom of vessel is:
View SolutionAn orifice of area 10 sq.mm is made at the bottom of a vessel cotaining water to a height of 10m above the orifice. What is the force on the vessel
View SolutionA vessel filled with water stands on a table. In this side, the vessel has a small orifice arranged at a distance 25 cm from the bottom of the vessel and at a distance 16 cm from the level of water which is kept constant. The horizontal distance from the orifice at which the jet of water fall on the table is
View Solution

