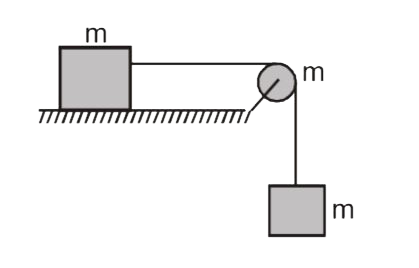
A system consists of three masses m1,m2 and my connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction = μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m, is mi (Assume m1=m2=m3=m)

g(1−gμ)9
2gμ3
g(1−2μ)3
g(1−2μ)2
The correct Answer is:C
Force of friction on mass
m2=μm2g
force of friction on mass
m3=μm3g
force of friction on mass
m3=μm3g
let a be common acceleration of the system
∴a=m1g−μm2g−μm3gm1+m2+m3
here m1=m2−m3−m
∴a=mg−μg−μgm+m+m=mg−2μmg3m=g(1−2μ)3
hence the downward acceleration of mass m1 is g(1−2μ)3

Similar Questions
A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View Solution
Knowledge Check
A system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
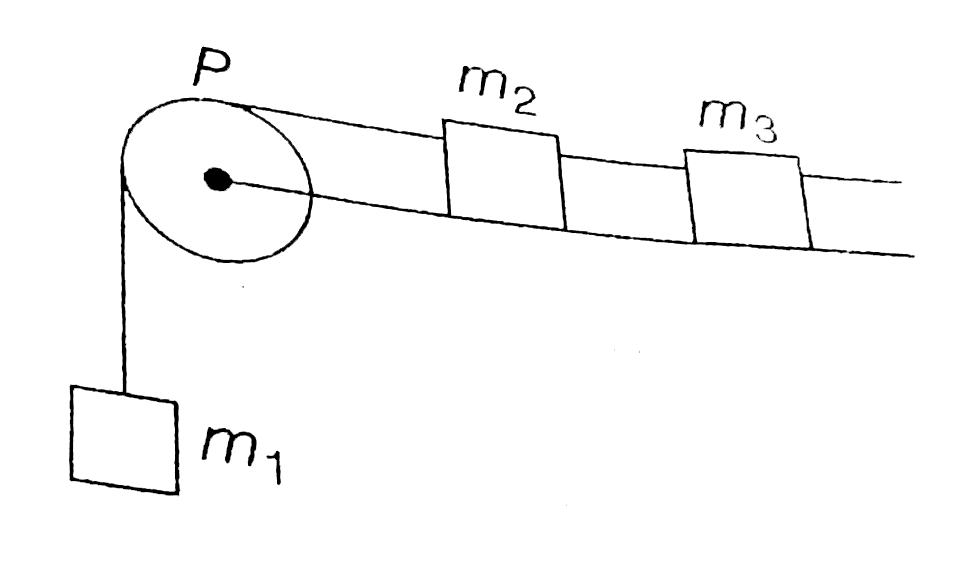 Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ) The pulley is frictionless and of negligible mass. The (Assume m1=m2=m3=m).
 Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2Two bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
A(a) (m1−m2m1+m2)gB(b) (m1−m2m1+m2)2gC(c) m1gm1+m2D(d) m2gm1+m2
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
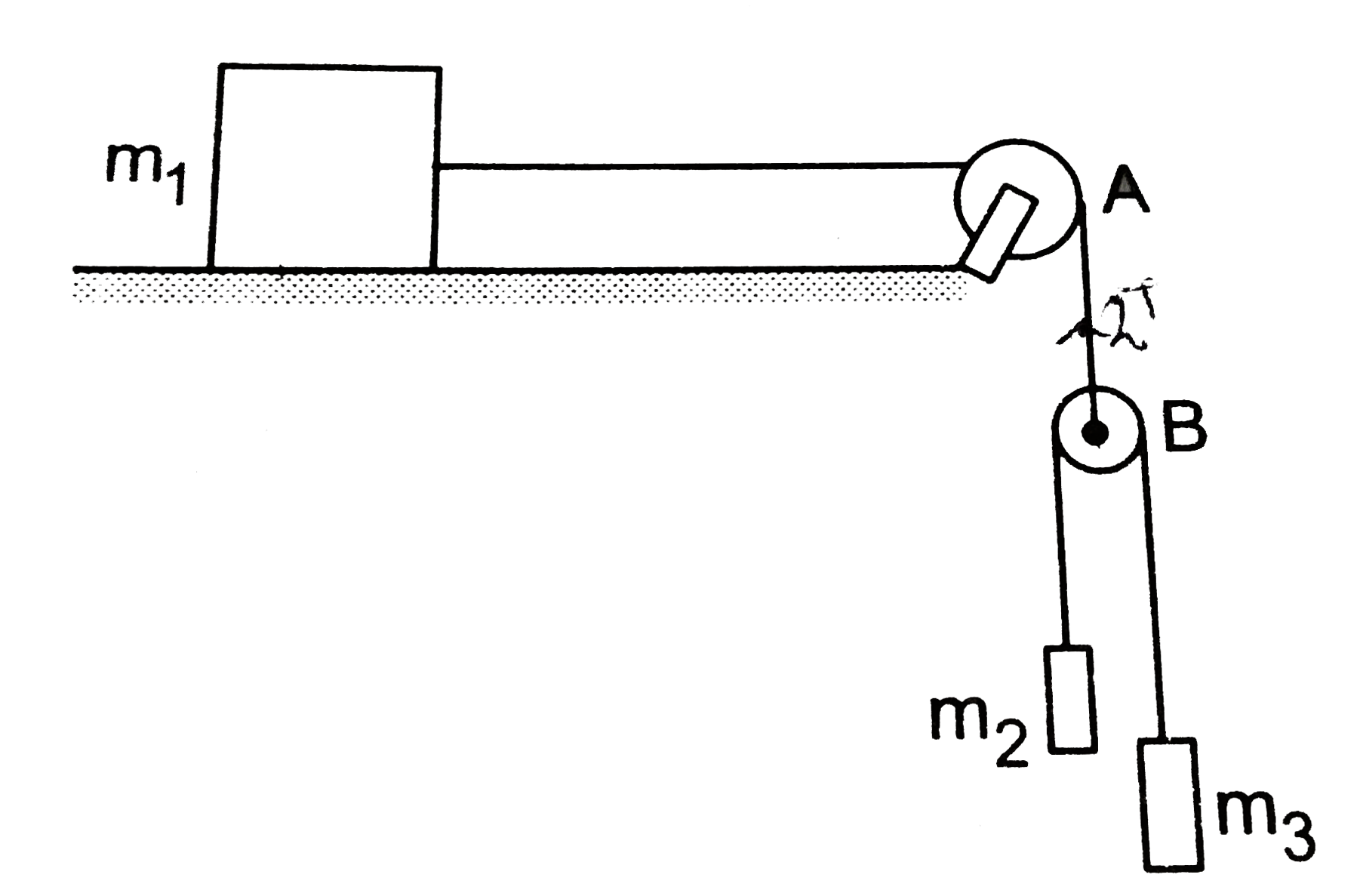
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1

View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solution

