∣∣ ∣∣11+ac1+bc11+ad1+bd11+ae1+be∣∣ ∣∣=
1
0
3
a+b+c
The correct Answer is:B
Step by step video, text & image solution for |(1,1+ac,1+bc),(1,1+ad,1+bd),(1,1+ae,1+be)|= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सारणिक तथा आव्यूह BOOK - ERRORLESS HINDICHAPTER - सारणिक तथा आव्यूह EXERCISE - Solved Multiple Choice Questions ( रैखिक समीकरणों का निकाय कुछ विशेष सारणिक, सारणिक का अवकलन तथा समाकलन)
50 Videos
- सारणिक तथा आव्यूह BOOK - ERRORLESS HINDICHAPTER - सारणिक तथा आव्यूह EXERCISE - Solved Multiple Choice Questions ( आव्यूह के प्रकार, आव्यूह का बीजगणित)
130 Videos
- सारणिक तथा आव्यूह BOOK - ERRORLESS HINDICHAPTER - सारणिक तथा आव्यूह EXERCISE - JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (Matrix Match type questions)
4 Videos
- सरल रेखा BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (Matrix Match type questions)
4 Videos
Similar Questions
a का वह मान जिसके लिये समीकरण निकाय a3x+(a+1)3y+(a+2)3z=0,ax(a+1)y+(a+2)z=0,x+y+z=0 का एक अशून्य हल है
View Solutionयदि M=[1223] और M2−λM−I2=0 तब λ=
View Solutionइस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
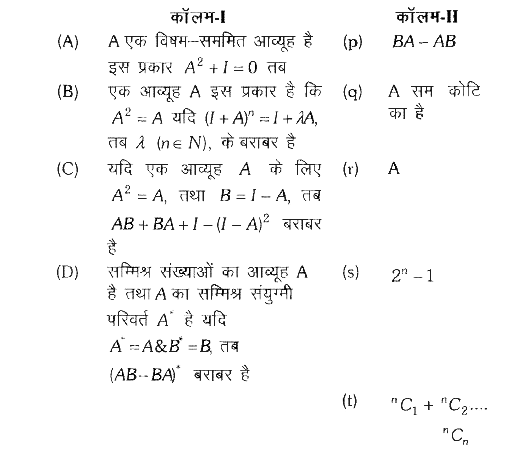
View Solution
View SolutionIf A=[(1,-1),(-1,1)] and B=[(1,1),(1,1)], prove that AB is null matrix.
View SolutionThe value of Δ=∣∣ ∣∣11+ac1+bc11+ad1+bd11+ae1+be∣∣ ∣∣, is
View SolutionThe value of ∣∣ ∣ ∣∣1 1 111+x 11 11+y∣∣ ∣ ∣∣is
View SolutionΔ=∣∣ ∣∣11+ac1+bc11+ad1+bd11+ae1+be∣∣ ∣∣ is independent of
View Solutionयदि A=[1−1−11] तथा B=[1111]: तो आव्यूह AB होगा -
View Solutionयदि A=[1−1−11] तथा B=[1111] तो सिद्ध कीजिए की AB शून्य आव्यूह है।
View Solution∣∣ ∣ ∣∣1 1 111+x 11 11+y∣∣ ∣ ∣∣
View SolutionΔ=∣∣ ∣∣11+ac1+bc11+ad1+bd11+ae1+be∣∣ ∣∣ is independent of
View Solution∣∣ ∣∣11+ac1+bc11+ad1+bd11+ac1+bc∣∣ ∣∣=0
View SolutionFind the product [−1−1−11][1111]
View SolutionThe rank of ⎡⎢⎣1−1111−1−111⎤⎥⎦ is
View Solution

