How does Ampere-Maxwell law explain the flow of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.
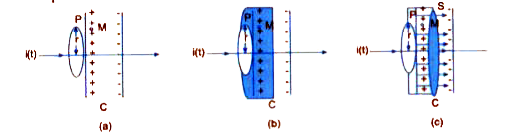
Consider charging of a parallel plate capacitor by a time-varying current iw Let us find the magnetic field at a point P in a region outside the capacitor. For this we consider a plane circular loop of radius r whose plane is perpendicular to the direction of the current carrying wire and which is centred symmetrically with respect to the wire [Fig]. Using symmetry condition and applying Ampere.s circuital law, we have
B(2πr)=μ0i(t) ....(i)
However, if we consider a different surface, having the same boundary [either as shown in Fig. or Fir. and apply Ampere.s circuital law as before, we find
B(2πr)=μ0(0)=0 ....(ii)
It is because nocurrent passes through the surface of Figs. and 8.04. It causes a contradiction because we get a finite value of magnetic field B by doing calculation in one way and zero value of B by doing calculation in another way. To remove this contradiction Maxwell introduced the concept of displacement current
iD=∈0dϕEdt, where dϕEdt is the rate of change of electric flux between the plates of given capacitor.
Now, the Ampere - Maxwell.s circuital law is expressed as
∮→B.→dl=μ0[i(t)+iD]
Thus, Ampere - Maxwell law successfully explains the flow the current through a capacitor when it is being charged (or discharged) by a battery.
Similar Questions
How does Ampere-Maxwell law explain the flow the of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.
View SolutionA parallel capacitor is being charged by an external source. Show that the sum of conductor current and displacement current has the same value everywhere in the circuit.
View Solution
Knowledge Check
An amperes is a rate of flow of electric current of
Aone faraday per secondBone coulomb per secondCone coulomb per minutesDone faraday per minutesAssertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge
Reason : The displacement current arises in the region in which the electric field is constant with time.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are falseThe conduction current in ideal case through a circuit is zero when charge on capacitor is
AzeroBmaximumCany transient valueDdepends on capacitor used
What is displacement current and write the modified Ampere's circuital law.
View SolutionWrite an expression for the heat produced when an electric current is passed through it.
View SolutionA parallel plate capacitor has capacitance 1μF . Deteremine the displcement current in the capacitor if rate of change of voltage between of 1A flows through it ?
View Solutionn electrons flow through a cross-section of a conductor in time t. If the charge on an electron is e, write an expression for the current in the conductor.
View SolutionA capacitor, made of two parallel plates each of plate are A and separation d, is being charged by an external a.c. source. Show that the displacement current inside the capacitor is the same as the current charging the capacitor.
View Solution

