Two masses m1 and m2 are suspended from a spring of spring constant 'K'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
√km2,m1gk
√m2k,km1g
√km2,km1g
√m2k,m1gk
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:PRACTICE EXERCISE - SIMPLE PENDULUM
Explore 22 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 12 Videos
- PHYSICAL WORLDBook:AAKASH SERIESChapter:PHYSICAL WORLDExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
A hollow sphere of simple pendulum is first filled with mercury and then with water. The time periods are in the ratio if their densities are in the ratio 13.6 :1
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find the amplitude and the time period of the motion of the block.

View SolutionWhat is Physics ?
View SolutionTwo masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
View SolutionTwo masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
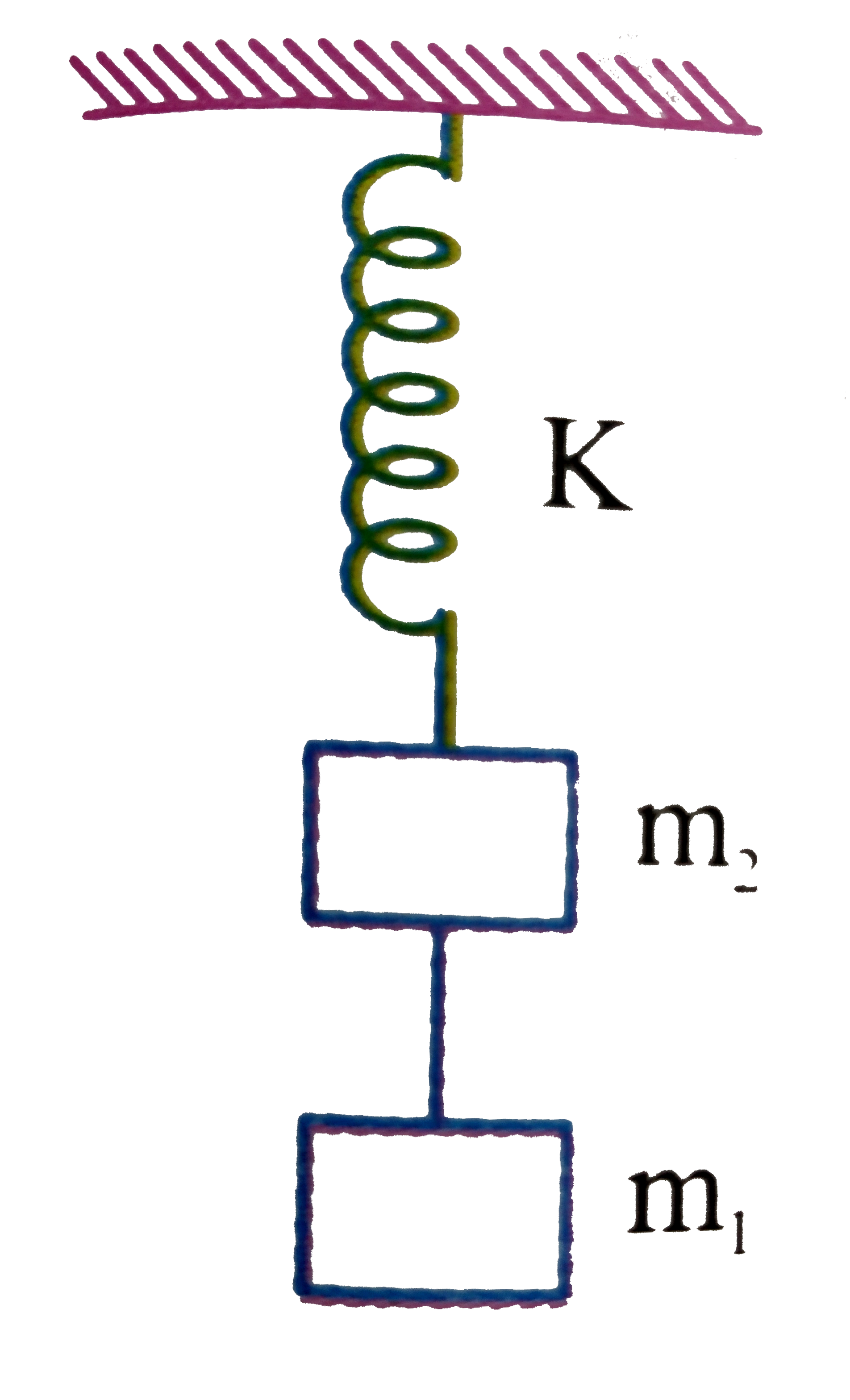
View SolutionTwo mass m_(1) and m_(2) are suspended from a massless spring of force constant k. When the masses are in equilibrium, m_(1) is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionTwo masses m1=1.0kgandm2=0.5kg are suspended together by a massless spring of force constant, k=12.5Nm−1. When they are in equillibrium position, m1 is gently removed. Calculate the angular frequency and the amplitude of oscillation of m2. Given g=10ms−2.
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
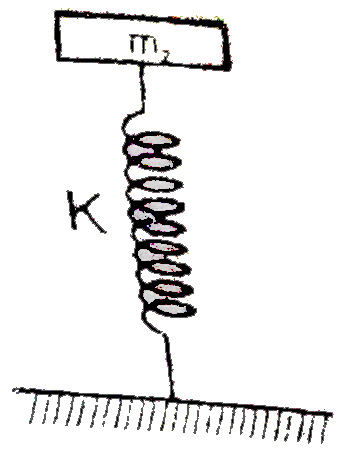
View SolutionTwo masses m_(1) and m_(2) are suspended together by a massless spring of constant K. When the masses are in equilibrium, m_(1) is removed without disturbing the system. Then the angular frequency of oscillation of m_(2) is -
View Solutionदो द्रव्यमान m1 व m2 एक द्र्व्यमाणहीन स्प्रिंग से जिसका बल नियतांक k है , लटके हैं। जब दोनों द्रव्यमान साम्यावस्था में हैं, m1 को धीरे से हटा दिया जाता है। m2 के दोलन की कोणीय आवृत्ति तथा आयाम ज्ञात कीजिए ।
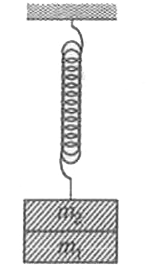
View SolutionTwo masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
View SolutionTwo masses m1 and m2 are suspended from a spring of spring constant 'k' . When the masses are in equilibrium , m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
View SolutionTwo masses m_(1) and m_(2) are suspended from a spring of spring constant 'k' . When the masses are in equilibrium , m_(1) is gently removed. The angular frequency and amplitude of oscillation of m_(2) will be respectively
View SolutionTwo masses m_(1) and m_(2) are suspended w together by a light spring of spring constant k as shown in figure. When the system is in equilibrium, the mass m_(1) is removed without disturbing the system. As a result of this removal, mass m_(2) performs simple harmonic motion. For this situation mark the correct statement(s).
View Solution

