Read the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage: For an LCR series circuit driven with an alternating voltage of amplitude Vmand angular frequency oo, the current amplitude is given as
Im=Vmz=Vm√R2+(XL−XC)2=Vm√R2+(Iω−1cω)2
If ω is varied then for a particular frequency ω0,XC=XL and then Z = R and hence, Im=VmR is maximum. This frequency is called the resonant frequency. The resonant frequency ω0=1√LC = Resonance of a LCR series a.c. circuit is said to be sharping current amplitude Im falls rapidly on increasing/decreasing the angular frequency from its resonant value 0. Mathematically, sharpness of resonance is measured by the quality factor of the circuit, which is given as:
Q=ωLR=1R√LC
(e) An alternating series LCR circuit consists of an
inductance of 10 mH, a capacitance of 100 uF and a resistance of 5 Ω. Compute its resonance frequency w, as well as the Q-factor.
Here, L = 10 mH = 0.01 H, C = 100 μF=100×10−6F and R = 5Ω
∴ Resonant frequency ω0=1√LC=1√0.01×100×10−6=100s−1
and Q-factor =ω0LR=1000×0.015=2
Topper's Solved these Questions
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:MULTIPLE CHOICE QUESTIONS
Explore 34 Videos
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:FILL IN THE BLANKS
Explore 11 Videos
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:ADDITIONAL EXERCISES
Explore 13 Videos
- ATOMSBook:U-LIKE SERIESChapter:ATOMSExercise:SELF ASSESSMENT TEST (SECTION C)
Explore 2 Videos
Similar Questions
Read the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage: For an LCR series circuit driven with an alternating voltage of amplitude Vmand angular frequency oo, the current amplitude is given as
Im=Vmz=Vm√R2+(XL−XC)2=Vm√R2+(Iω−1cω)2
If ω is varied then for a particular frequency ω0,XC=XL and then Z = R and hence, Im=VmR is maximum. This frequency is called the resonant frequency. The resonant frequency ω0=1√LC = Resonance of a LCR series a.c. circuit is said to be sharping current amplitude Im falls rapidly on increasing/decreasing the angular frequency from its resonant value 0. Mathematically, sharpness of resonance is measured by the quality factor of the circuit, which is given as:
Q=ωLR=1R√LC
(b) How does impedance of the circuit changes with ω
View SolutionRead the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage: For an LCR series circuit driven with an alternating voltage of amplitude Vmand angular frequency oo, the current amplitude is given as
Im=Vmz=Vm√R2+(XL−XC)2=Vm√R2+(Iω−1cω)2
If ω is varied then for a particular frequency ω0,XC=XL and then Z = R and hence, Im=VmR is maximum. This frequency is called the resonant frequency. The resonant frequency ω0=1√LC = Resonance of a LCR series a.c. circuit is said to be sharping current amplitude Im falls rapidly on increasing/decreasing the angular frequency from its resonant value 0. Mathematically, sharpness of resonance is measured by the quality factor of the circuit, which is given as:
Q=ωLR=1R√LC
(d) How is a resonant circuit is utilised to tune a TV set at a particular channel ?
View Solution
Knowledge Check
For an RLC circuit driven with voltage of amplitude vm and frequency ω0=1√LC the current exibits resonance. The quality factor, Q is given by :
ACRω0Bω0LRCω0RLDR(ω0C)In the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
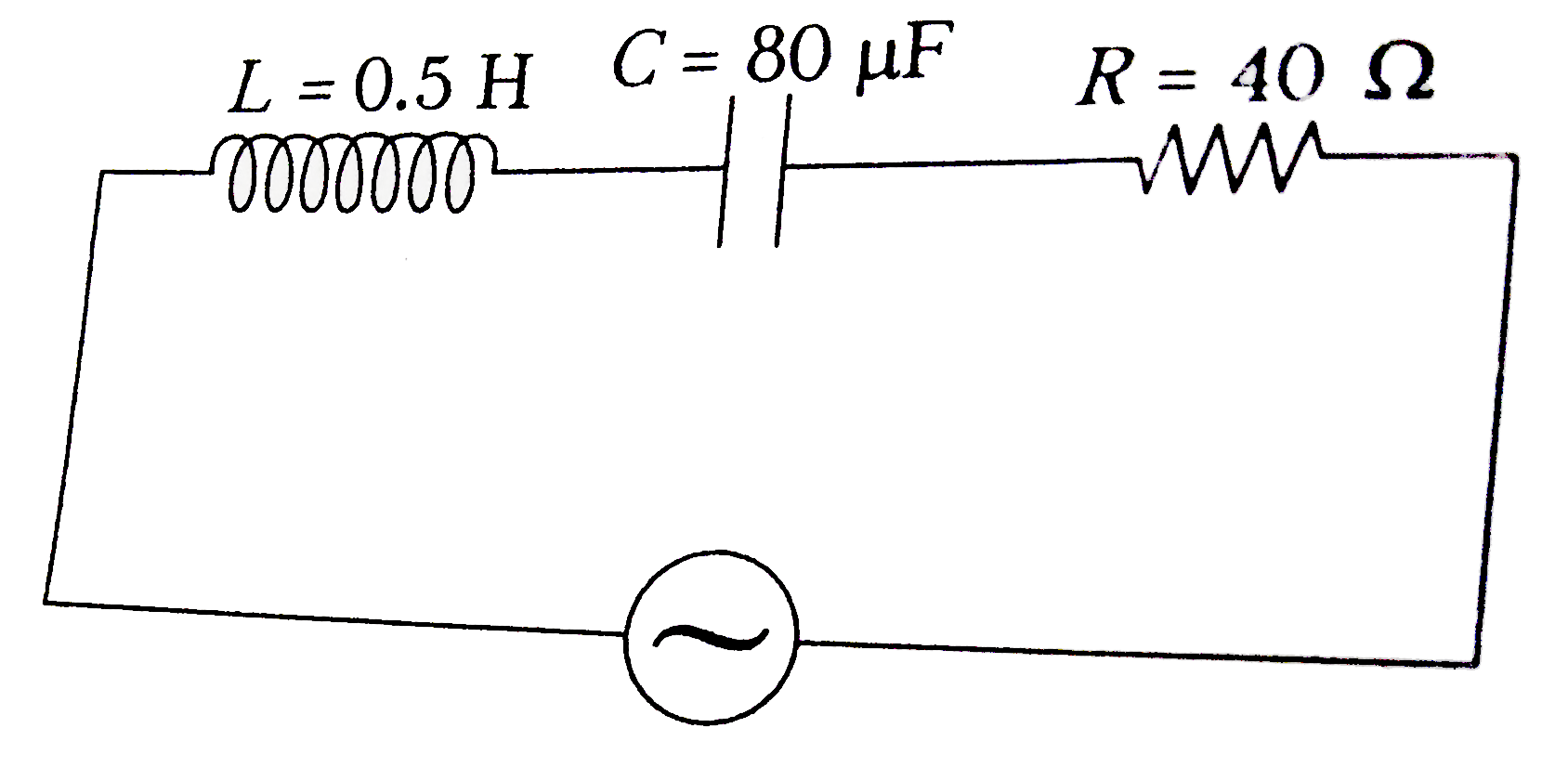 A20Ω and 4.2 AB30Ω and 6.9 AC25Ω and 5.8 AD40Ω and 5.75 A
A20Ω and 4.2 AB30Ω and 6.9 AC25Ω and 5.8 AD40Ω and 5.75 AAn inductor has a resistance R inductance L. It is connected to an A.C source of e.m.f. EV and angular frequency ω then the current Iv in the circuit is
AEVωLBEVRCEV√R2+ω2L2D√(EVR)2+(EVωL)2
Read the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage: For an LCR series circuit driven with an alternating voltage of amplitude Vmand angular frequency oo, the current amplitude is given as
Im=Vmz=Vm√R2+(XL−XC)2=Vm√R2+(Iω−1cω)2
If ω is varied then for a particular frequency ω0,XC=XL and then Z = R and hence, Im=VmR is maximum. This frequency is called the resonant frequency. The resonant frequency ω0=1√LC = Resonance of a LCR series a.c. circuit is said to be sharping current amplitude Im falls rapidly on increasing/decreasing the angular frequency from its resonant value 0. Mathematically, sharpness of resonance is measured by the quality factor of the circuit, which is given as:
Q=ωLR=1R√LC
(c) What is the nature of reactance in the circuit when (i) ω<ω0 and (ii) ω>ω0 ?
View SolutionRead the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage: For an LCR series circuit driven with an alternating voltage of amplitude Vmand angular frequency oo, the current amplitude is given as
Im=Vmz=Vm√R2+(XL−XC)2=Vm√R2+(Iω−1cω)2
If ω is varied then for a particular frequency ω0,XC=XL and then Z = R and hence, Im=VmR is maximum. This frequency is called the resonant frequency. The resonant frequency ω0=1√LC = Resonance of a LCR series a.c. circuit is said to be sharping current amplitude Im falls rapidly on increasing/decreasing the angular frequency from its resonant value 0. Mathematically, sharpness of resonance is measured by the quality factor of the circuit, which is given as:
Q=ωLR=1R√LC
(a) (a) Draw graphs showing variation of current amplitude of a LCR series circuit with frequency w of driving ω<ω0 , alternating voltage.
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
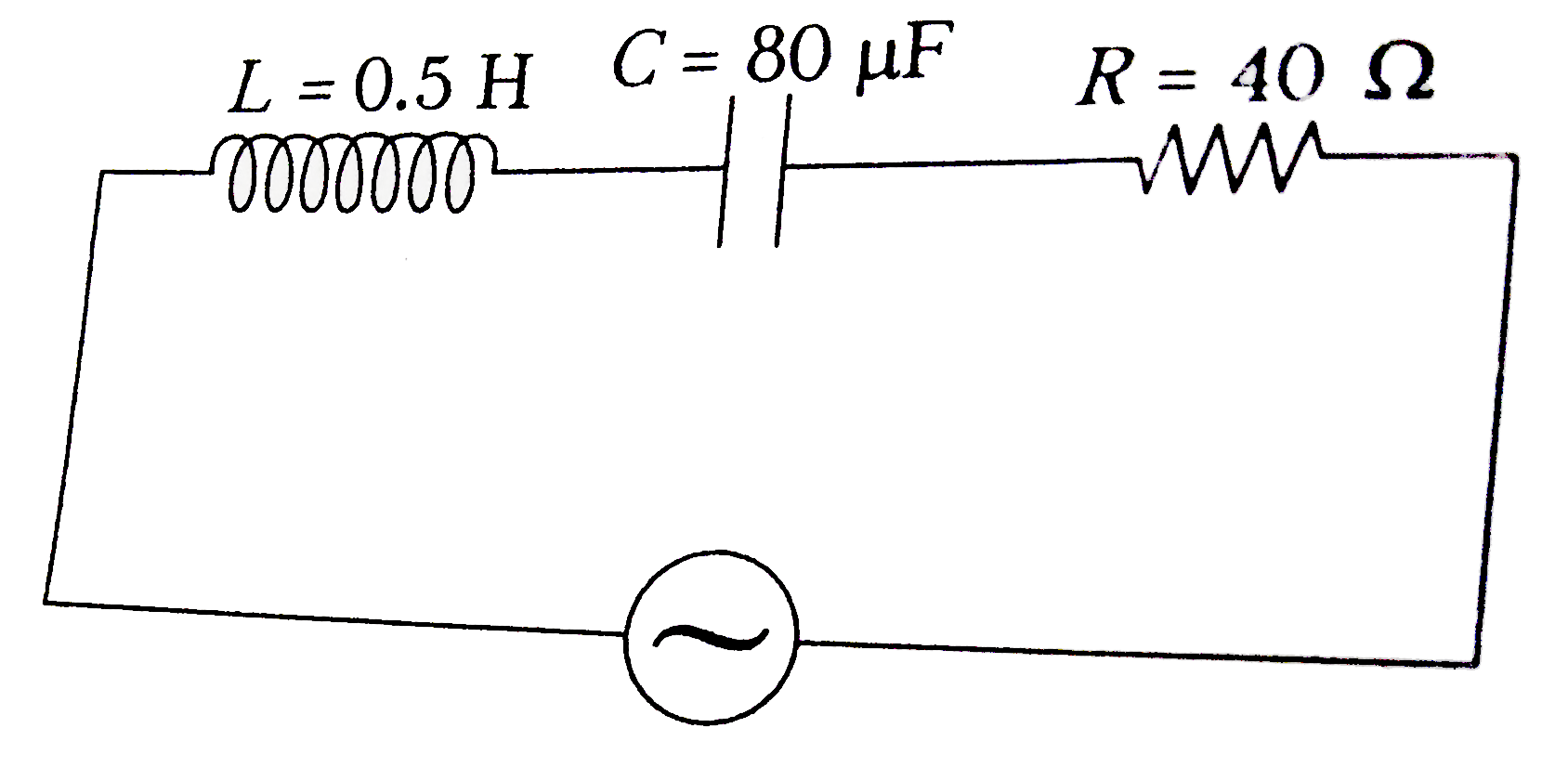
View SolutionIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
View SolutionThe frequency of an alternating voltage is 50 cycles/sec and its amplitude is 120V. Then the r.m.s value of voltage is
View Solution

