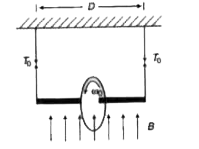
Ring of radius R having uniformly distributed charge Q is mounted on a rod suspended by two identical strings as shown in fig. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and the ring is rotated at constant angular velocity Ω. Find the maximum Ω with which the ring can be rotated if the strings can withstand a maxiumum tension 3T02
T0=ωQBR2Dorω=DT0QBR2
Similar Questions
एक वलय जिसकी त्रिज्या R है, उस पर आवेश एकसमान रूप से वितरित है। यह वलय दो एक जैसी डोरियों द्वारा निलम्बित छड़ पर चढ़ा हुआ है। साम्यावस्था में डोरियों में तनाव T0 है। एक ऊर्ध्वाधर चुम्बकीय क्षेत्र को प्रारम्भ करने पर वलय कोणीय चाल ω से घूर्णन करने लगता है। यदि डोरियों के तनाव की अधिकतम सीमा 3T02 है तो ω का अधिकतम मान जिससे कि वलय घूम सके क्या होगा?
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA ring of radius R is with a uniformly distributed charge on it. A charge q is now placed at the centre of the ring. Find the increment in tension in the ring.
View SolutionA ring of radius R having unifromly distributed charge Q is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and ring is rotated at constant angular velocity ω. Find the maximum ω with which the ring can be rotated if the strings can withstand a maximum tension of 3T0/2.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA string has a linear mass density mu . The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity omega Q. The tension developed in the string is
View SolutionA string has a linear mass density mu . The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity omega Q. The velocity of a transverse wave set up in the string, with respect to the string is
View Solution

