A wave propagates on a string in positive x-direction with speed of 40 cm/s. The shape of string at t = 2s is y=10cosx5 where x and y are in centimeter. Find the wave equation and draw the graph of y vs x.
10cos(x5−8t+16∘), 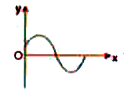
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBook:AAKASH SERIESChapter:WAVE MOTION AND SOUNDExercise:PROBLEMS (LEVEL - I)
Explore 60 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
Explore 10 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:PROBLEMS (LEVEL - II)
Explore 20 Videos
Similar Questions
For the wave y=5sin30π[t−(x/240)], where x and y are in cm and t is in seconds, find the
Displacement when t = 0 and x = 2cm
View SolutionA source emitting sound of frequency 180 Hz is placed in front of a wall at a distance of 2m from it. a detector is also placed in front of the wall at the same distance from it. The minimum distance between the source and the detector is x mtrs for which the detector shows a maxima of sound. Speed of sound in air = 360 m/s
View SolutionIn Young's double slit experiment the y co-ordinates of central maxima and 10th maxima are 2 cm and 5 cm respectively. When the YDSE apparatus is immersed in a liquid of refractive index 1.5. Find the corresponding y co-ordinates.
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by y =(1)/(1 + x^(2)) at t = 0 and y =(1)/(1 +(x - 1)^(2)) at t =2s where, x and y are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by y=Ae^((-t/t-x/A)^(2)) where A=5mm, T=1.0 s and lambda=8.0 cm (a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View SolutionA sinusoidal wave having wavelength of 6 m propagates along positive x direction on a string. The displacement (y) of a particle at x = 2 m varies with time (t) as shown in the graph (a) Write the equation of the wave (b) Draw y versus x graph for the wave at t = 0
View SolutionThe shape of a wave propagating in the positive x or negative x-direction is given y=1√1+x2 at t=0 and y=1√2−2x+x2 at t=1s where x and y are in meters the shape the wave disturbance does not change during propagation find the velocity of the wave
View Solutionएक डोरी में X-दिशा में गतिमान तरंग का समीकरण y=3sin[314t−3.14x] है, जहाँ y तथा x सेमी में एवं t सेकण्ड में है । ज्ञात कीजिये -
(i) डोरी में तरंग की चाल, (ii) तरंग की आवृत्ति, (iii) तरंग की तरंग-दैर्ध्य (iv) डोरी के किसी कण की अधिकतम चाल ।
View SolutionA transverse harmonic wave on a string is described by y(x,t)=30sin(36t+0.018x+π4)where x and y are in cm and t is in s.The positive direction of x is from left to right.
Is this a travelling wave or a stationary wave ? If it is travelling, what are the speed and direction of its propagation ?
View SolutionThe equation of stationary wave along a stretched string is given by y=5sin(πx)3cos40πt where x and y are in centimetre and t in second. The separation between two adjacent nodes is :
View SolutionThe equation of a transverse travelling wave on a string is y = 2 cos pi (0.5xx - 200t) , where x and y are in cm and r in sec. Then the velocity of propagation of the wave is
View SolutionLet y=11+x2 at t=0 s be the amplitude of the wave propogating in the positive x-direction. At t=2 s, the amplitude of the wave propogating becomes y=11+(x−2)2. Assume that the shape of the wave does not change during propogation. The velocity of the wave is
View SolutionThe equation of a wave moving on string y=8sin{π(0.002x−4t)} where x , y are in centimeter and t in seconds . The velocity of the wave is ……… .
View SolutionA transverse harmonic wave on a string is descrbed by y(x,t)=3.0sin(36t+0.018x+π4) where x and y are in cm and t is in s. The position direction of x is from left to right.
View SolutionA wave propagates on a string in positive x-direction with a speed of 40 cm/s. The shape of string at t = 2 s is y=10cosx5 where x and y are in centimeter. The wave equation is
View Solution

