माना L1:a1x+b1y+c1=0,L2:a2x+b2y+c2=0 तथा L3:a3x+b3y+c3=0 है।
कथन-I :L1:L2:L3 तीन सर्वांगसम रेखायें है, तो ∣∣
∣∣a1b1c1a2b2c2a3b3c3∣∣
∣∣=0 होगा। क्योंकि
कथन-II : यदि ∣∣
∣∣a1b1c1a2b2c2a3b3c3∣∣
∣∣=0 हो, तो रेखायें L1,L2 तथा L3 संगामी होगी।
कथन-I सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है : कथन-II, कथन-I का सही स्पष्टीकरण नहीं है|
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन- असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for माना L_(1) :a_(1)x + b_(1)y + c_(1)=0, L_(2):a_(2)x + b_(2)y + c_(2)=0 तथा L_(3):a_(3)x + b_(3)y +c_(3)=0 है। कथन-I :L_(1) : L_(2) : L_(3) तीन सर्वांगसम रेखायें है, तो |{:(a_(1),b_(1),c_(1)),(a_(2),b_(2),c_(2)),(a_(3),b_(3),c_(3)):}|=0 होगा। क्योंकि कथन-II : यदि |{:(a_(1),b_(1),c_(1)),(a_(2),b_(2),c_(2)),(a_(3),b_(3),c_(3)):}|=0 हो, तो रेखायें L_(1),L_(2) तथा L_(3) संगामी होगी। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023टॉपर्स ने हल किए ये सवाल
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 1:)
3 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 2:)
3 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column)
2 Videos
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [B]
10 Videos
- लघुगणक BOOK - ALLEN HINDICHAPTER - लघुगणक EXERCISE - DO YOURSELF -6
2 Videos
समान प्रश्न
एक गतिमान बिन्दु का बिन्दुपथ वह पथ है, जो वह बिन्दु दिये गए एक या अधिक ज्यामितिय प्रतिबंधों में, मम्करता हुआ बनाता है। बिन्दु का बिन्दुपथ ज्ञात करने के लिए बिन्दु के निर्देशांक (h, k) मानते है, तथा प्रश्न में दिये गये प्रतिबन्धों प्लेतथाk के मध्य सम्बन्ध ज्ञात करने का प्रयास करते है। यदि इस विधि में कोई भी चर होता है तो हम उसे विलुप्त करते है। अन्त में ईको x से तथाk को 7 से पुनः स्थापित करके ज्ञात करते है जो कि बिन्दु का अभीष्ठ बिन्दुपथ है, जो कि वy में समीकरण होगी।
त्रिभुज जिसके शीर्ष (acost, asint), (bsint, – bcost) तथा (1,0) है, जहाँ t एक प्राचल है, के केन्द्रक का बिन्दुपथ है|
View Solutionनिर्देशी तल के बिन्दुओं P≡(x1,y1) तथा Q≡(x2,y2) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P,Q)=|x1−x2|+|y1−y2|
माना O≡(0,0),A≡(1,2),B≡(2,3) तथा C≡(4,3),x−y तल में चार स्थिर बिन्दु है।
माना R(x, y) इस प्रकार है कि नई दूरी के अनुसार R बिन्दुओं o तथा A से समान दूरी पर है तथा यदि 0≤x<1 व 0≤y<2 तब R एक रेखाखण्ड पर स्थित होगा जिसकी समीकरण है-
View Solutionनिम्न प्रश्नों में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमे (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा नामित किया गया है।स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
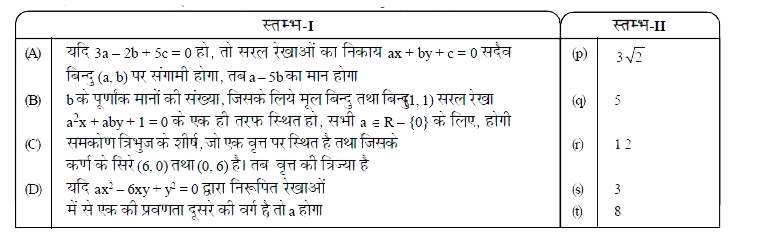
View Solutionयदि 2n∑r=0ar(x−2)r=2n∑r=0br(x−3)r और सभी k≥n के लिए ak=1 तो दिखाइए की bn=2n+1Cn+1
View Solutionहल कीजिए :|x+3|=2(5−x)
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=5, then the value of
Δ=∣∣ ∣∣b2c3−b3c2a3c2−a2c3a2b3−a3b2b3c1−b1c3a1c3−a3c1a3b1−a1b3b1c2−b2c1a2c1−a1c2a1b2−a2b1∣∣ ∣∣ is
View SolutionStatement -1 Consider the determinant
Δ=∣∣ ∣ ∣∣a1+b1x2a1x2+b1c1a2+b2x2a2x2+b2c2a3+b3x2a3x2+b3c3∣∣ ∣ ∣∣=0,
where ai,bi,ci∈ R (i=1,2,3) and x∈ R
Stement -2 If ∣∣ ∣∣a1b2c3a2b2c2a3b3c3∣∣ ∣∣ =0, then Δ =0
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣≠0∣∣ ∣∣a1+b1xa1x+b1c1a2+b2xa2x+b2c2a3+b3xa3x+b3c3∣∣ ∣∣=0 then x=
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=Δ, then ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣=
View SolutionShow that ∣∣ ∣∣a1b1−c1−a2−b2c2a3b3−c3∣∣ ∣∣=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣
View SolutionThe determinant
∣∣ ∣∣b1+c1c1+a1a1+b1b2+c2c2+a2a2+b2b3+c3c3+a3a3+b3∣∣ ∣∣
View SolutionIf Ai,Bi,Ci are the cofactors of ai,bi,ci respectively,i=1,2,3 in Δ=∣∣ ∣∣a1b2c1a2b2c2a3b3c3∣∣ ∣∣show that ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣=Δ0
View SolutionIf Ai,Bi,Ci are the cofactors of ai,bi,ci respectively,i=1,2,3 in Δ=∣∣ ∣∣a1b2c1a2b2c2a3b3c3∣∣ ∣∣show that ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣=Δ0
View SolutionIf A=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣andB=∣∣ ∣∣c1c2c3a1a2a3b1b2b3∣∣ ∣∣ then
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=5, then the value of ∣∣ ∣∣b2c3−b3c2a3c2−a2c3a2b3−a3b2b3c1−b1c3a1c3−a3c1a3b1−a1b3b1c2−b2c1a2c1−a1c2a1b2−a2b1∣∣ ∣∣ is
View Solution

