निर्देशी तल के बिन्दुओं P≡(x1,y1) तथा Q≡(x2,y2) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P,Q)=|x1−x2|+|y1−y2|
माना O≡(0,0),A≡(1,2),B≡(2,3) तथा C≡(4,3),x−y तल में चार स्थिर बिन्दु है।
माना T(x.y) इस प्रकार है कि नई दूरी के अनुसार T, बिन्दुओं O तथा C से समान दूरी पर है तथा यदि प्रथम चतुर्थांश में स्थित है, तब निश्चित लम्बाई की रेखा खण्ड तथा अनन्त किरणो का संयोजन है, जिसका चिम्ति चित्र है-
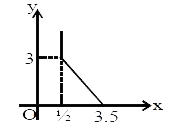

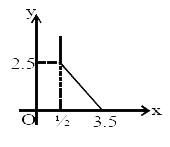
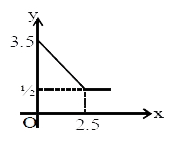
The correct Answer is:A
Step by step video, text & image solution for निर्देशी तल के बिन्दुओं P-= (x_(1),y_(1)) तथा Q-= (x_(2),y_(2)) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P, Q) = |x_1 - x_2| + |y_1 - y_2| माना O -= (0, 0), A -= (1, 2), B -= (2, 3) तथा C -= (4, 3), x - y तल में चार स्थिर बिन्दु है। माना T(x.y) इस प्रकार है कि नई दूरी के अनुसार T, बिन्दुओं O तथा C से समान दूरी पर है तथा यदि प्रथम चतुर्थांश में स्थित है, तब निश्चित लम्बाई की रेखा खण्ड तथा अनन्त किरणो का संयोजन है, जिसका चिम्ति चित्र है- by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023समान प्रश्न
वह अनुपात ज्ञात कीजिए जिसमें बिंदुओं P(x1,y1,z1) तथा Q(x2,y2,z2) को मिलाने वाली रेखा , समतल ax + by + cz + d = 0 व्दारा विभाजित होती है ।
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionदो रेखाएं x−31=y+13=z−6−1 तथा x+57=y−2−6=z−34 बिन्दु R पर काटती है । बिन्दु R के XY तल के प्रतिबिम्ब के निर्देशांक है
View Solutionमाना C1 तथा C2 क्रमश: वृत्तों x2+y2−2x−2y−2=0 तथा x2+y2−6x−6y+14=0 के केन्द्र है । यदि P तथा Q इन वृत्तों के प्रतिच्छेद बिन्दु है , तो चतुर्भुज PC1QC2 का क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View SolutionIf the hyperbola xy=c2 intersects the circle x2+y2=a2 is four points P(x1,y1),Q(x2,y2),R(x3,y3)andS(x4,y4) then show that
(i) x1+x2+x3+x4=0
(ii) y1+y2+y3+y4=0
(iii) x1x2x3x4=c4
(iv) y1y2y3y4=c4
View SolutionPoint of reference floor P-= (x_(1),y_(1)) And Q-= (x_(2),y_(2)) For, the new distance d (P, Q) is defined by the following formula. d(P, Q) = |x_1 - x_2| + |y_1 - y_2| agreed O -= (0, 0), A -= (1, 2), B -= (2, 3) And C -= (4, 3), x - y The floor has four fixed points. Let R (x, y) be such that R is equally spaced from the points o and A as per the new distance and if 0 le x lt 1 and 0 le y lt 2 Then R will be located on a line whose equation is-
View SolutionPoint of reference floor P-= (x_(1),y_(1)) And Q-= (x_(2),y_(2)) For, the new distance d (P, Q) is defined by the following formula. d(P, Q) = |x_1 - x_2| + |y_1 - y_2| agreed O -= (0, 0), A -= (1, 2), B -= (2, 3) And C -= (4, 3), x - y The floor has four fixed points. Let S (x, y) be such that according to the new distance, S is equally spaced from the points O and B. And if x ge 2 and 0 le y lt 3 Is, then the locus of S will be -
View Solution

