Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two springs are K1 and K2 respectively. The period of vertical oscillations of the system will be:
18π√K1+K2
8π√K1+K2K1K2
π2√K1−K2
π2√K1K2
The correct Answer is:B
the two springs are in series. Therefore, the period,
T=2π√MK=2π√M(K1+K2K1K2) As M=16kg,T=8π√K1+K2K1K2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE 2 MARKS)
15 Videos
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
10 Videos
- NUCLEAR PHYSICBOOK - MTG-WBJEECHAPTER - NUCLEAR PHYSICEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
5 Videos
- PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMBOOK - MTG-WBJEECHAPTER - PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
Similar Questions
Knowledge Check
A mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
AT=2π√mk1−k2BT=2π√mk1k2k1+k2CT=2π√mk1+k2DT=2π√m(k1+k2)k1k2A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
Find the spring constant of a system made up of two springs joined in parallel.
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
View SolutionTwo particles A and B of equal masses are suspended from two massless springs of spring constants K1andK2 respectively. If the maximum velocities during oscillations are equal. the ratio of the amplitude of A and B is
View SolutionA mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be

View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
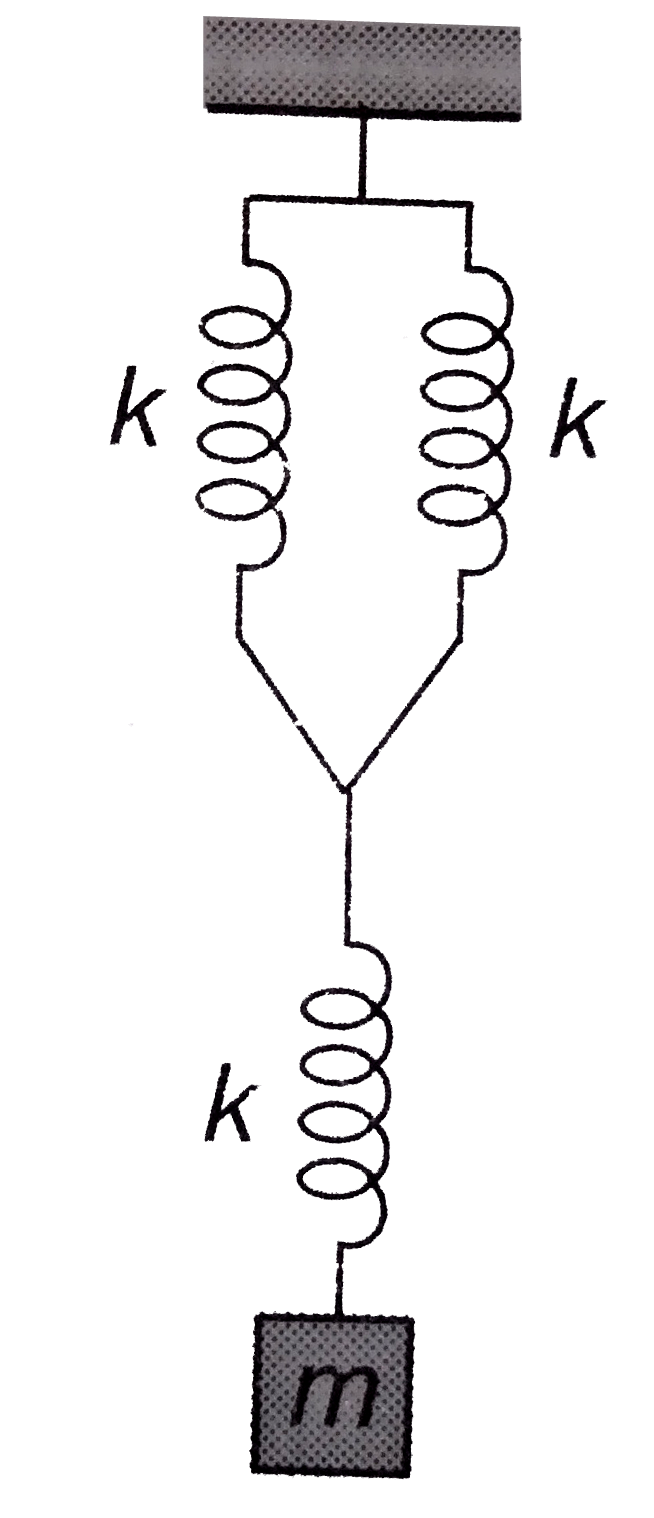
View Solution


