truck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
15 m/s
20 m/s
25 m/s
30 m/s
The correct Answer is:B
To solve the problem, we need to find the speed at which the bullet hits the truck. We will follow these steps:
Step 1: Convert the muzzle velocity of the bullet from km/h to m/s
The muzzle velocity is given as 90 km/h. We can convert this to meters per second using the conversion factor:
Velocity in m/s=Velocity in km/h×518
Calculating this gives:
90km/h×518=25m/s
Step 2: Determine the speed of the bullet relative to the ground
The car is moving at a speed of 10 m/s, and it fires the bullet in the same direction. Therefore, the speed of the bullet relative to the ground is the sum of the bullet's muzzle velocity and the speed of the car:
Bullet speed relative to ground=Muzzle velocity+Car speed
Substituting the values:
Bullet speed relative to ground=25m/s+10m/s=35m/s
Step 3: Determine the speed of the truck relative to the ground
The truck is moving at a speed of 15 m/s.
Step 4: Calculate the relative speed of the bullet with respect to the truck
Since both the bullet and the truck are moving in the same direction, the speed of the bullet as observed from the truck is the difference between the bullet's speed relative to the ground and the truck's speed:
Relative speed of bullet with respect to truck=Bullet speed relative to ground−Truck speed
Substituting the values:
Relative speed of bullet with respect to truck=35m/s−15m/s=20m/s
Final Answer
The speed with which the bullet hits the truck is 20 m/s.
---
The muzzle velocity is given as 90 km/h. We can convert this to meters per second using the conversion factor:
The car is moving at a speed of 10 m/s, and it fires the bullet in the same direction. Therefore, the speed of the bullet relative to the ground is the sum of the bullet's muzzle velocity and the speed of the car:
The truck is moving at a speed of 15 m/s.
Since both the bullet and the truck are moving in the same direction, the speed of the bullet as observed from the truck is the difference between the bullet's speed relative to the ground and the truck's speed:
The speed with which the bullet hits the truck is 20 m/s.
Similar Questions
What is the momentum of a 100000 kg truck whose velocity is 20m/s ?
View SolutionA car of mass one metric ton travelling at 32m/sc dashes into the rear of a truck of mass 8000kg moving in the same direction with a velocity of 4m/s After the collision the car bounces back wards with a velocity of 8m/s What is the velocity of the truck after the impact ?
View Solution
Knowledge Check
Theif's car is moving with a speed of 10 m/s. A police van chasing this car with a speed of 5 m/s fires a bullet at the theif's car with muzzle velocity 72 km/h. Find the speed with which the bullet will hit the car-
A10 m/sB20 m/sC15 m/sD25 m/sA police jeep is chasing with, velocity of 45km/h a thief in another jeep moving with velocity 153km/h. Police fires a bullet with muzzle velocity of 180m/s. The velocity it will strike the car of the thief is.
A150m/sB27m/sC450m/sD250m/s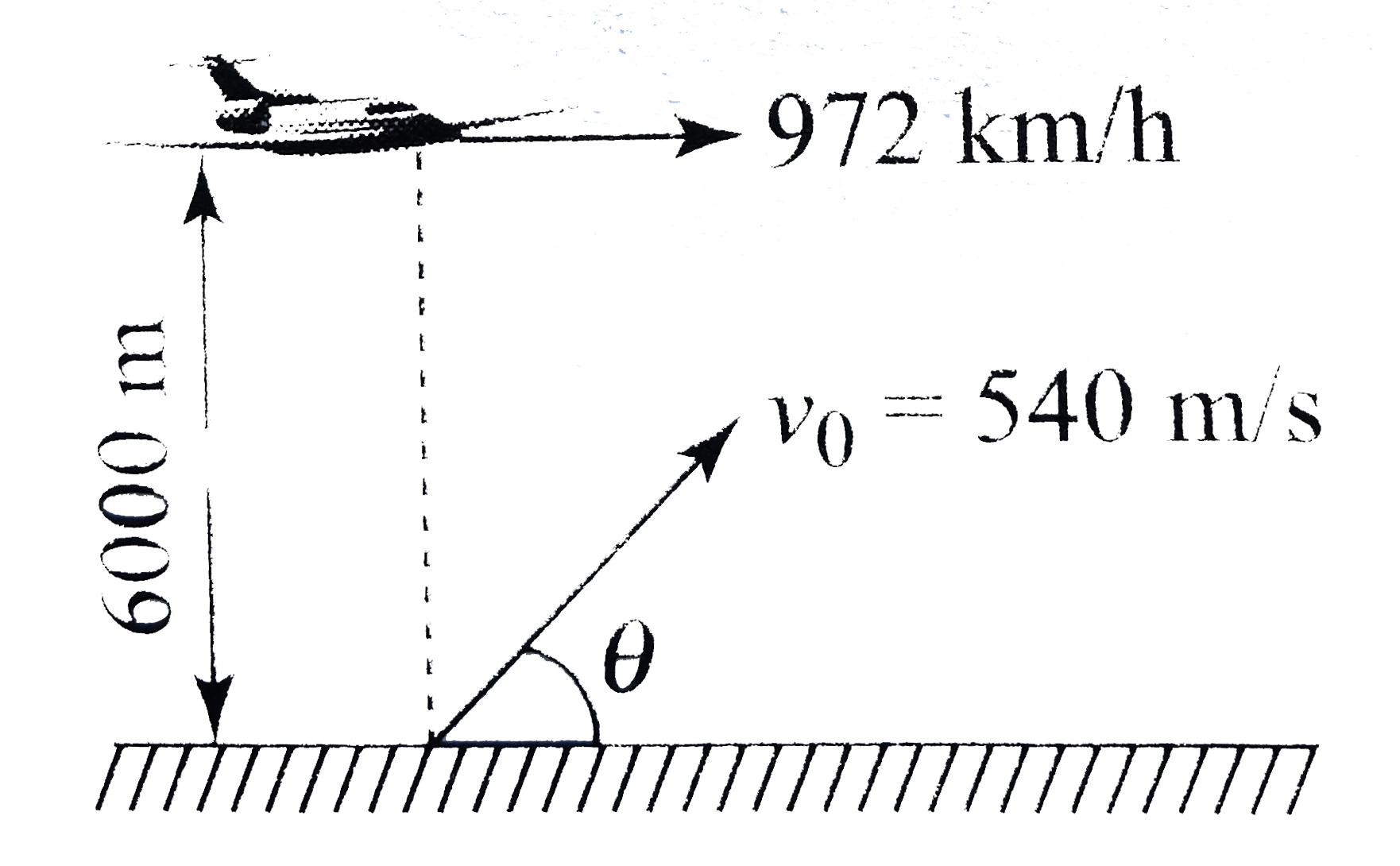
An aircraft moving with a speed of 1000 km/h is at a heirgh of 6000 m, just overhead of an anti-aircraft gun. If the muzzle velocity of the gun is 540 m/s, the firing angle θ for the bullet to hit the aircraft should beA73∘B30∘C60∘D45∘
In fig. shown, the speed of the truck is v to the right. Find the speed with which the block is moving up at θ=60∘.

View SolutionA police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .
.
View SolutionThe rear view mirror of a car is a plane mirror. A driver is reversing his car at a speed of 2m/s. The driver sees in his rear view mirror the image of truck parked behind his car. The speed at which of the image of the truck appears to approach the driver will be
View SolutionA car travels a distance AB at a speed of 40 km/hr and returns to A at a speed of 30 km/hr. What is the average speed for the whole journey?
View SolutionThe distance between two trucks moving towards each other is decreasing at the rate of 10m/s. If these trucks travel with same speeds in same direction the separation increases at the rate of 5m/s. The speeds of the trucks are :
View Solution

