यदि f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩e−|x|,−5<x<0−e−|x−1|+e−1+1,0≤x<2e−|x−2|,2≤x<4 अंतराल (−5,4) में f(x) की संतता और अवकलनीयता की जाँच कीजिये।
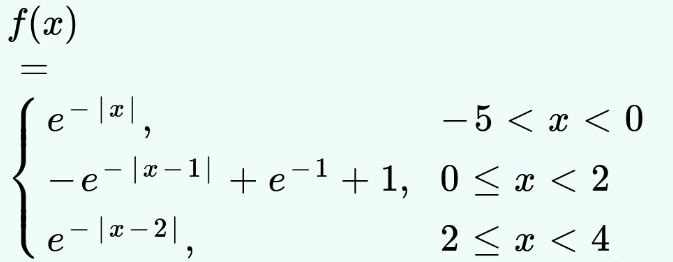
हम जानते हैं कि, |x−1|= {x−1x≥1−x+1x<1
अतः
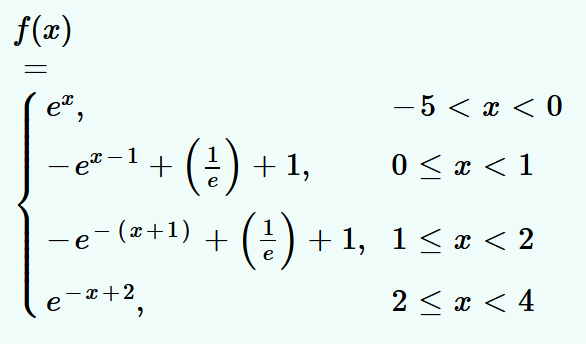
अतः 0,1,2 पर संतता की जांच करनी है।
x=0 पर,
LHL=limx→0ex
=e0
LHL=1
RHL
=limx→0−ex−1+(1e)+1
RHL=−e0−1+(1e)+1
RHL=−e−1+(1e)+1
RHL=−1e+1e+1=1
तथा f(0)=−e−1+(1e)+1
=1
स्पष्ट है कि,
LHL=RHL=f(x)=1
अतः x=0 पर संतत हैं|
इसी प्रकार x=1 पर,
LHL
=limx→1−ex−1+(1e)+1
LHL=−e1−1+(1e)+1
LHL=−e0+(1e)+1
LHL=−1+1e+1=1e
RHL
=limx→1−e−x+1+(1e)+1
RHL=−e−1+1+(1e)+1
RHL=−1+1e+1=1e
तथा f(1)=1e
स्पष्ट है कि,
LHL=RHL=f(x)=1e
अतः x=1 पर संतत हैं|
इसी प्रकार,
x=2 पर,
LHL
=limx→2−e−x+1+(1e)+1
LHL=−e−2+1+(1e)+1
LHL=−1e+(1e)+1
LHL=1
RHL
=limx→2−e−x+2
RHL=−e−2+2=1
RHL=−e0=1
RHL=1
तथा f(2)=1
स्पष्ट हैं की,
LHL=RHL=f(x)
अतः x=2 पर संतत हैं|
इसलिए f(x) संतत हैं, x=0,1,2
अवकलनीयता की जाँच,
चूंकि फलन हर जगह संतत हैं अतः फलन का हम सीधा अवकलन कर सकते हैं|
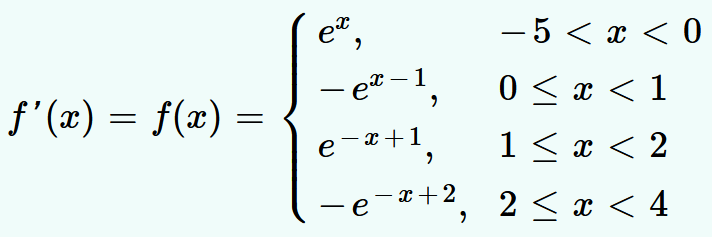
x=0 पर अवकलनीयता की जाँच,
LHD=limx→0ex
LHD=e0=1
RHD=limx→0−ex−1
RHD=−e0−1
RHD=−e−1=−1e
स्पष्ट हैं की,
LHD≠RHD अतः x=0 पर, अवकलनीय नहीं हैं|
इसी प्रकार x=1 पर
LHD=limx→1−ex−1
LHD=−e1−1
LHD=−e0=−1
RHD=limx→1e−x+1
RHD=e−1+1
RHD=e0=1
स्पष्ट है कि,
LHD≠RHD अतः x=1 पर, अवकलनीय नहीं हैं|
इसी प्रकार x=2 पर,
LHD=limx→2e−x+1
LHD=e−2+1= 1/e
RHD=limx→2−e−x+2
RHD=−e−2+1=−1e
स्पष्ट है कि,
LHD≠RHD अतः x=2 पर, अवकलनीय नहीं हैं|
अतः 0,1,2 पर संतत हैं परंतु अवकलनीय नहीं हैं|
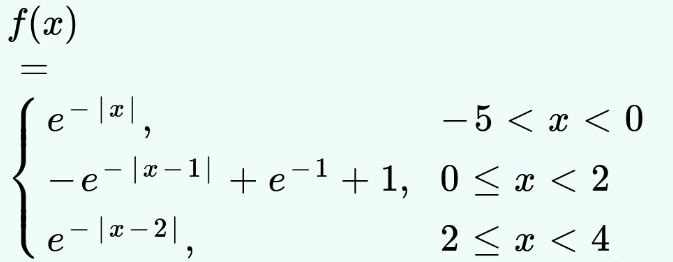
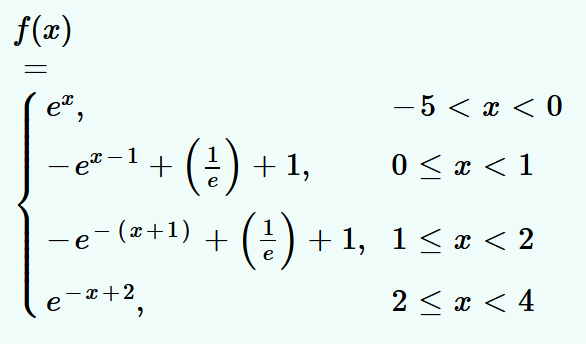
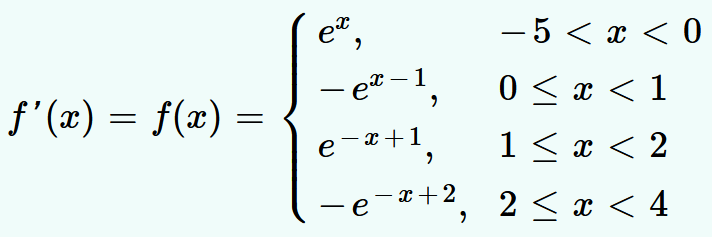
Similar Questions
The cumculative distribution function of a discrete random variable is given by
F(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0for −∞<x<012for 0≤x<135for 1≤x<245for 2≤x<3910for 3≤x<41for 4≤x<∞
Find (i) the probability mass function (ii) P(X<3) and (iii) P(X≥2).
View SolutionIf f(x)=∫ex(x−1)(x−2)dx, then show that f(x) is a decreasing function 1<x<2.
View Solutionफलन के लिए रोल प्रमेय की सत्यता की जाँच कीजिए
f(x)=⎧⎪⎨⎪⎩x2+10≤x≤1यदि3−x1<x≤2
View Solutionयदि f(x)=|logex|={−logexयदि0<x<1logexयदिx≥1 तो दिखाइए कि फलन x=1 पर अवकलनीय नहीं है।
View SolutionFind the value of a,b if f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩ae1/|x+2|−12−e1/|x+2|;−3<x<−2b;x=−2sin(x4−16x5+32);−2<x<0 is continuous at x=−2.
View SolutionIf f(x)={:{(x", for " 0 le x lt 1),(2", for " x=1),(x+1", for " 1 lt x le 2):} , then f is
View Solutionमाना एक फलन f(x)=⎡⎢⎣1−x0≤x≤1x+21<x<24−x2≤x≤4 हो तो f(f(x)) और Limx→2f(f(x)) का मान ज्ञात कीजिये
View Solution
