Show that the lines x+2=0,y−1=0 and 2x+3y+1=0 are concurrent.
The correct Answer is:Hence the three lines are concurrent.
Topper's Solved these Questions
- STRAIGHT LINESBook:AAKASH SERIESChapter:STRAIGHT LINESExercise:ADDITIONAL SOLVED EXAMPLES
Explore 12 Videos
- STRAIGHT LINESBook:AAKASH SERIESChapter:STRAIGHT LINESExercise:EXERCISE 3.1 (VERY SHORT ANSWER QUESTIONS)
Explore 11 Videos
- STRAIGHT LINESBook:AAKASH SERIESChapter:STRAIGHT LINESExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II (ADVANCED) PRACTICE SHEET (ADDVANCED)) (Comprehension Type Questions)
Explore 6 Videos
- REVISION EXERCISEBook:AAKASH SERIESChapter:REVISION EXERCISEExercise:PROPERTIES OF TRIANGLES
Explore 57 Videos
- TANGENT AND NORMAL Book:AAKASH SERIESChapter:TANGENT AND NORMAL Exercise:ADVANCED SUBJECTIVE TYPE QUESTIONS
Explore 48 Videos
Similar Questions
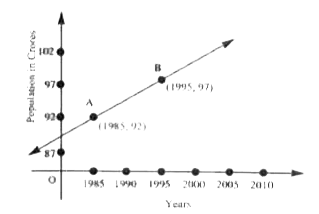
Consider the following population and year graph, find the slope of the line AB and using it, find what will be the population in the year 2010?
View SolutionFind the slope of the line whose inclination is
30∘
View SolutionLet A(0,0), B (5,0), C (5,3) and D(0,3) be the vertice of rectiangle ABCD , If P is a variable point lying inside the rectangle ABCD and d (P,L) denotes perpendicular distance of point P from line L
If ≤min{d(P,BC),d(P,CD),d(P,AD)}, then area of the region in which P lies is (in sq. units
View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)
View SolutionThe lines 2x+y−1=0, ax+3y−3=0 and 3x+2y−2=0 are concurrent for -
View SolutionIf the lines x +3y -9 = 0, 4x + by -2 = 0 and 2x -y -4 = 0 are concurrent , the b is equal to
View SolutionShow that the lines2x+y−3=0,3x+2y−2=0 and 2x−3y−23=0 are concurrent and find the point fo concurrency.
View SolutionShow that the lines 2x+y−3=0,3x+2y−2=0and2x−3y−23=0 are concurrent and find the point of concurrency.
View SolutionShow that the straight lines :
x−y−1=0, 4x+3y=25 and 2x−3y+1=0 are concurrent.
View SolutionState whether the st.lines :
x−y−1=0, 4x+3y=25 and 2x−3y+1=0 are concurrent or not ?
View SolutionIf the lines x - y - 1 = 0, 4x + 3y = k and 2x – 3y +1 = 0 are concurrent, then k is
View SolutionIf the lines x−y−1=0,4x+3y=k and 2x−3y+1=0 are concurrent, then k is
View SolutionIf the lines x+3y−9=0,4x+by−2=0 and 2x−y−4=0 are concurrent, then b equals
View SolutionIf the lines x−y+1=0,2x+3y+2=0andax+by−2=0 are concurrent, then 5x+10=0 passes through the point
View Solution

