Zदिशा के अनुदिश गतिमान एक समतल वैधुतचुमबकीय तरंग को E=E0sin(kz–εt)ˆIतथाB=B0sin(kz–εt)ˆj द्वारा वर्णित किया गया है। दर्शाइए कि
(i) तरंग का औसत ऊर्जा घनत्व है।
μav=14E0E20+14.B20μ0
(ii) तरंग की काल – ओसत तीव्रता है।
Iav=12CE0E20
(i) Eक्षेत्र का येागदार हैं EE=12ε0E2
B=क्षेत्र का योगदान है μB=12.B2μ0
कुल ऊर्जा घनत्व μ=μE+μB=12ε0E2+12.B2μ0
E2 तथाB2 के मान प्रत्येक बिन्दु तथा प्रत्येक क्षण पर परिवर्ती होते हैं अत:E∘तथाB2 के प्रभावी मान उनके कालिक मान है।
(B−2)ε=E20[sin2(kz−εt)]ε
sin2θ तथाcos2θ के ग्राफ आकृति में समरूप है लेकिन π/2 से स्थानान्तरित है। अतsin2θ तथाcos2θ के औसत मान भी π के किसी पूर्ण संख्यिकी गुणज के लिए समान है।
तथाsin2θ+cos2θ=
अत:सममिति से sin2θ का औसत =cos2θ का औसत =12
(E2)ε=12E∘0“and“(B2)ε=12B20
समीकरण 1 में प्रस्थान करने पर
μ=14ε0E2+14B20μ
(ii) इमें ज्ञात है। E0B0=c तथाc=1√μ0ε0∴,14.B204μ0=E204μ0μ0ε0=14ε0E20
με=14ε0E20+14ε0=12ε0E20तथाIε=μεc=12ε0E20
Similar Questions
A plane EM wave travelling along z - direction is desctribed vec(E )=E_(0)sin(kz - omega t)hat(i) and veC(B)=B_(0)sin (kz - omega)hat(j) . Show that The average energy density of the wave is given by U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0)) .
View SolutionA plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20.
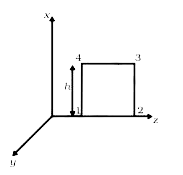
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
View SolutionThe magnetic field of a plane electromagnetic wave is given by: →B=B0ˆi−[cos(kz−ωt)]+B1ˆjcos(kz+ωt) where B0=3×10−5T and B1=2×10−6T. The rms value of the force experienced by a stationary charge Q=10−4C at z=0 is close to:
View Solutionनिर्वात में z दिशा के अनुदिश गमनशील एक समतल वैधुतचुबकीय तरंग को E=E0sin(kz−εt)ˆI तथा B=B0sin(kz−εt)ˆj द्वारा प्रदर्शित किया गया हैं
(i)चित्र में दर्शाइए गए आयताकार लूप 1234 पर ∫E.d1 का मान ज्ञात कीजिए
(ii) लूप 1234 द्वारा घिरे पुष्ठ के लिए ∫B.ds का मान ज्ञात कीजिए।
(iii) समीकरण ∫E.d1=−dϕBdt का उपयोग करके सिध्द कीजिए E0B0=c
(iv) इसी प्रकार की प्रकिया तथा समीकरण OB.d1=μ0I+E0dϕEdt का उपयोग करके सिध्द कीजिए कि c=1√μ0E0
View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionAn electric field vec(E)=E_(0) hat(i)+E_(0) hat(j) exists in space. The flux through triangular loop with vertices at ((a)/(2), 0,0) , ((a)/(2), 0, a) and ((a)/(2) , a, (a)/(2)) is (E_(0) a^(2))/(b) . Find b .
View Solution

