The initial velocity vi required to project a body vertically upward from the surface of the earth to reach a height of 10R, where R is the radius of the earth, may be described in terms of escape velocity ve such that vi=√xy×ve. The value of x will be __________ .
The correct Answer is:10
To solve the problem of finding the initial velocity vi required to project a body vertically upward from the surface of the Earth to reach a height of 10R (where R is the radius of the Earth), we will use the principle of conservation of energy.
1. Understanding the Problem:
We need to find the initial velocity vi such that a body reaches a height of 10R. At this height, the body's velocity will be zero.
2. Using Conservation of Energy:
The total mechanical energy at the surface of the Earth (initial) must equal the total mechanical energy at the height of 10R (final).
Initial Energy=Final Energy
The initial energy consists of kinetic energy and gravitational potential energy, while the final energy at height 10R consists only of gravitational potential energy since the kinetic energy is zero at the maximum height.
3. Writing the Energy Equations:
- Initial Energy:
Ei=12mv2i−GMmR
- Final Energy:
Ef=−GMm11R
(At height 10R, the distance from the center of the Earth is R+10R=11R)
4. Setting Up the Equation:
Setting the initial energy equal to the final energy:
12mv2i−GMmR=−GMm11R
5. Simplifying the Equation:
- Multiply through by 11R to eliminate the denominators:
11R(12mv2i)−11GMm=−GMm
- Rearranging gives:
11R(12mv2i)=10GMm
6. Canceling Mass:
Since m appears in all terms, we can cancel it out:
11R(12v2i)=10GM
7. Solving for v2i:
12v2i=10GM11R
v2i=20GM11R
8. Relating to Escape Velocity:
The escape velocity ve is given by:
ve=√2gR=√2GMR
Therefore, GM=v2eR2.
9. Substituting for GM:
Substitute GM in the equation for v2i:
v2i=20⋅v2eR211R
v2i=10v2e11
10. Finding vi:
Taking the square root gives:
vi=√1011ve
11. Identifying x and y:
The problem states that vi=√xyve. From our equation:
√1011=√xy
Thus, x=10 and y=11.
Final Answer:
The value of x will be 10.
We need to find the initial velocity vi such that a body reaches a height of 10R. At this height, the body's velocity will be zero.
The total mechanical energy at the surface of the Earth (initial) must equal the total mechanical energy at the height of 10R (final).
- Initial Energy:
Ei=12mv2i−GMmR
- Final Energy:
Ef=−GMm11R
(At height 10R, the distance from the center of the Earth is R+10R=11R)
Setting the initial energy equal to the final energy:
12mv2i−GMmR=−GMm11R
- Multiply through by 11R to eliminate the denominators:
11R(12mv2i)−11GMm=−GMm
- Rearranging gives:
11R(12mv2i)=10GMm
Since m appears in all terms, we can cancel it out:
11R(12v2i)=10GM
12v2i=10GM11R
v2i=20GM11R
The escape velocity ve is given by:
ve=√2gR=√2GMR
Therefore, GM=v2eR2.
Substitute GM in the equation for v2i:
v2i=20⋅v2eR211R
v2i=10v2e11
Taking the square root gives:
vi=√1011ve
The problem states that vi=√xyve. From our equation:
√1011=√xy
Thus, x=10 and y=11.
The value of x will be 10.
Topper's Solved these Questions
Similar Questions
A transmitter circuit used for transmission of EM waves having wavelength 960m If capacitor used in circuit was of 2.56microF, then the self inductance of the inductor coil used in the circuit such that resonance occurs, is P⋅10−8 Find P
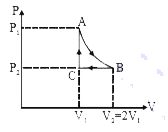
View Solutionn mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :
View SolutionThe ratio of escape velocity at earth (v_(e)) to the escape velocity at a planet (v_(y)) whose radius and density are twice
View SolutionThe escape velocity of a body from the surface of the earth is V_(1) and from an altitude equal to twice the radius of the earth, is, V_(2) . Then
View SolutionThe escape velocity from the surface of earth is V_(e) . The escape velocity from the surface of a planet whose mass and radius are 3 times those of the earth will be
View SolutionA body is imparted a velocity v from the surface of the earth. If v_(0) is orbital velocity and v_(e) be the escape velocity then for :
View SolutionA body is projected from the surface of the earth with thrice the escape velocity (V_(e)) from the surface of the earth. What will be its velocity, when it will escape the gravitational pull?
View SolutionThe escape velocity of a body from the earth is Ve. The escape velocity of a planet whose mass and radius are twice those of the earth is
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View SolutionA projectile is fired vertically upward from the surface of earth with a velocity K v_(e) where v_(e) is the escape velocity and K lt 1 . Neglecting air resistance, show that the maximum height to which it will rise measured from te centre of earth is R//(1-K^(2)) where R is the radius of the earth.
View SolutionA projectile is fired vertically upward from the surface of earth with a velocity K v_(e) where v_(e) is the escape velocity and K lt 1 . Neglecting air resistance, show that the maximum height to which it will rise measured from te centre of earth is R//(1-K^(2)) where R is the radius of the earth.
View SolutionA particle is given a velocity (v_(e ))/(sqrt(3)) in a vertically upward direction from the surface of the earth, where v_(e ) is the escape velocity from the surface of the earth. Let the radius of the earth be R. The height of the particle above the surface of the earth at the instant it comes to rest is :
View SolutionThe escape velocity from the surface of earth is Ve. The escape velocity from the surface of a planet whose mass and radius are 3 times those of the earth will be
View SolutionThe ratio of escape velocity at earth (v_(e)) to the escape velocity at a planet (v_(y)) whose radius and density are twice
View SolutionThe ratio of escape velocity at earth (v_(e)) to the escape velocity at a planet (v_(y)) whose radius and density are twice
View Solution

